Оглавление
Представляем вашему вниманию уникальный калькулятор теоремы Пифагора — вашего надежного помощника в мире математики. Этот инструмент разработан для того, чтобы облегчить расчеты и сделать процесс изучения и применения теоремы Пифагора как можно более доступным и понятным для каждого.
Что это за калькулятор?
В основе его работы лежит знаменитая теорема Пифагора, согласно которой в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Наш онлайн-калькулятор позволяет быстро находить длину неизвестной стороны треугольника, а также вычислять углы, площадь, периметр и высоту гипотенузы.
Преимущества использования:
- Простота и удобство: Интерфейс калькулятора интуитивно понятен, что делает его доступным для использования людьми любого возраста и уровня подготовки.
- Точность расчетов: Благодаря продвинутым алгоритмам, калькулятор обеспечивает высокую точность вычислений, что крайне важно для математических и инженерных расчетов.
- Экономия времени: С помощью этого калькулятора вы можете мгновенно получить результаты расчетов, минуя сложные и времязатратные процедуры ручного вычисления.
- Образовательная ценность: Использование калькулятора способствует лучшему пониманию принципов работы теоремы Пифагора, облегчая процесс обучения.
Как это работает?
Для начала работы с калькулятором достаточно выбрать, какую сторону треугольника вы хотите найти (a, b или c) и ввести известные значения остальных сторон. После нажатия на кнопку «Рассчитать», калькулятор мгновенно предоставит вам результат, включая длину искомой стороны, а также дополнительные параметры, такие как площадь и периметр треугольника.
Для кого этот калькулятор?
Он станет незаменимым инструментом для школьников и студентов, изучающих геометрию, а также для инженеров и всех, кто работает с математическими и физическими расчетами в своей профессиональной деятельности.
Применяя калькулятор теоремы Пифагора, вы сделаете свой учебный и профессиональный процесс более продуктивным и интересным. Попробуйте его сейчас и убедитесь в его полезности и удобстве!
Инструкция по заполнению формы калькулятора теоремы Пифагора
Эта инструкция поможет вам правильно заполнить форму калькулятора теоремы Пифагора. Она создана для упрощения процесса вычислений и делает его доступным даже для начинающих. Следуйте простым шагам, и вы быстро получите нужный результат.
Назначение полей
Выбор неизвестной стороны (a, b, c) — в этом разделе вы определяете, какую сторону треугольника хотите найти. Выбор осуществляется нажатием на соответствующую кнопку: «a», «b», или «c».
Ввод известных значений — в полях «a», «b», «c» вводятся числовые значения известных сторон треугольника. Одно из полей будет заблокировано в зависимости от вашего выбора в первом шаге.
Как заполнять
Выбор стороны для расчета: Первым делом определитесь, какую сторону треугольника вы хотите рассчитать. Нажмите на одну из кнопок: «a», «b», или «c». Это определит, какая сторона будет искомой.
Ввод данных: В оставшихся активных полях введите значения известных вам сторон треугольника. Например, если вы хотите найти сторону «a» и у вас есть значения для «b» и «c», вам нужно ввести эти значения в соответствующие поля.
Пример заполнения:
Если известно, что сторона «b» равна 4, а сторона «c» — 5, и вы хотите найти сторону «a», вам нужно:
- Нажать на кнопку «a» для её выбора как искомой.
- Ввести в поле «b» значение «4».
- Ввести в поле «c» значение «5».
Важные моменты
Вводите только числа: Убедитесь, что в поля ввода вы вводите только числовые значения. Использование букв или символов может привести к ошибке в расчетах.
Проверка на ошибки: Если при расчете появляется сообщение об ошибке, проверьте корректность введенных данных. Убедитесь, что значения соответствуют условиям теоремы Пифагора (сумма квадратов катетов равна квадрату гипотенузы).
Ознакомление с результатом: После нажатия на кнопку «Рассчитать», ознакомьтесь с предоставленными данными. Кроме искомой стороны, калькулятор может показать дополнительные параметры, такие как площадь и периметр треугольника.
Следуя этим рекомендациям, вы легко сможете использовать калькулятор теоремы Пифагора для решения своих задач. Надеемся, что данная инструкция окажется полезной и сделает процесс обучения более интересным и продуктивным.
Серия примеров использования калькулятора теоремы Пифагора
Эти примеры демонстрируют, как калькулятор теоремы Пифагора может быть использован в различных сферах жизни, от бытовых задач до более сложных инженерных и планировочных расчетов.
Определение высоты дерева
Постановка задачи: Вам необходимо определить высоту дерева, не имея возможности измерить его напрямую. Вы замерили расстояние от дерева до точки наблюдения на земле — 5 метров (катет b), и угол взгляда на вершину дерева — 45 градусов, что позволяет предположить, что высота дерева (катет a) равна расстоянию до него.
Шаги решения:
- Выберите «a» для расчета в калькуляторе.
- Введите значение «b» — 5 метров.
- Поскольку угол 45 градусов предполагает равенство катетов в прямоугольном треугольнике, введите «c» равное 5 метров, учитывая, что «c» — это гипотенуза, но для упрощения расчета в данном случае мы используем это приближение.
Результаты расчета: Калькулятор покажет, что высота дерева (a) приблизительно равна 5 метрам.
Применение на практике: Этот метод позволяет легко оценить высоту объектов, когда прямое измерение невозможно.
Расчет материалов для строительства крыши
Постановка задачи: Вам нужно рассчитать длину стропил для крыши дома. Известна ширина основания будущей крыши (8 метров), которая будет равна длине гипотенузы c треугольника, и высота подъема крыши от основания до вершины — 3 метра (катет a).
Шаги решения:
- Выберите «b» для расчета в калькуляторе, так как вам нужно найти длину другого катета.
- Введите «a» равное 3 метра и «c» равное 8 метров.
Результаты расчета: Калькулятор выдаст длину катета b, которая покажет необходимую длину стропил.
Применение на практике: Полученные данные помогут вам точно заказать или подготовить необходимое количество материала для стропил без излишков.
Планирование маршрута для туризма
Постановка задачи: Вы планируете пешеходный тур и хотите рассчитать реальное расстояние между двумя точками, которые разделены горой. Из карты вы узнали, что расстояние по прямой (гипотенуза c) составляет 10 км, а высота горы относительно вашего маршрута — 2 км (катет a).
Шаги решения:
- Выберите «b» для расчета, чтобы найти длину основания горы.
- Введите «a» равное 2 км и «c» равное 10 км.
Результаты расчета: Калькулятор покажет длину маршрута вдоль основания горы (b), что позволит вам более точно спланировать время путешествия.
Применение на практике: Эта информация поможет в планировании времени на прохождение маршрута, позволяя более точно распределить силы и время на отдых.
Таблица полезных сведений для использования калькулятора теоремы Пифагора
Эта таблица служит вспомогательным инструментом для тех, кто использует калькулятор теоремы Пифагора, облегчая понимание основных параметров и формул, необходимых для расчетов. Она будет полезна студентам, инженерам, архитекторам и всем, кто работает с геометрическими расчетами в своей профессиональной деятельности или повседневной жизни.
| Параметр | Описание | Формула | Пример использования |
|---|---|---|---|
| Длина стороны (a или b) | Длина одного из катетов прямоугольного треугольника. | a² + b² = c² | Для определения длины стропил крыши. |
| Длина гипотенузы (c) | Длина самой длинной стороны прямоугольного треугольника, противолежащая прямому углу. | c = √(a² + b²) | Для расчета расстояния по прямой между двумя точками. |
| Площадь треугольника | Площадь прямоугольного треугольника. | (a*b)/2 | Для расчета площади земельного участка или стен дома. |
| Периметр треугольника | Сумма длин всех сторон треугольника. | a + b + c | Для определения общей длины ограждения участка. |
| Высота гипотенузы | Расстояние от вершины, противолежащей гипотенузе, до гипотенузы. | (a*b)/c | Для определения высоты объекта, основание которого доступно для измерения. |
| Углы треугольника | Углы в прямоугольном треугольнике, включая прямой угол. | Косинус, синус, тангенс | Для нахождения углов наклона крыши или лестницы. |
Примечание к таблице:
- Формула представляет собой математическое выражение, используемое для расчета каждого параметра.
- Пример использования дает представление о практическом применении данных расчетов в реальной жизни или специализированных задачах.
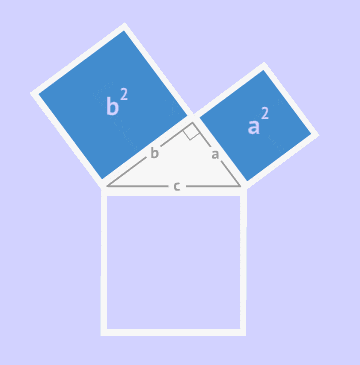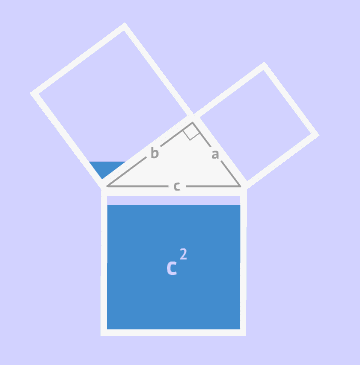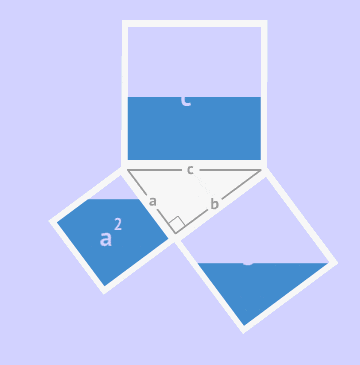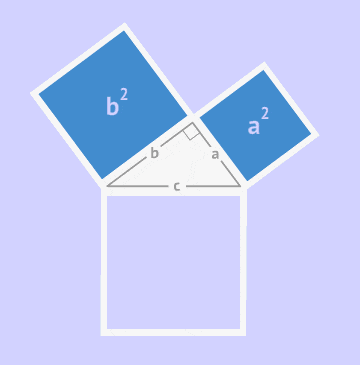
Доказательство теоремы Пифагора
Давайте разберемся, как доказать теорему Пифагора, рассматривая площади фигур.
Представим себе квадрат, длина стороны которого равна сумме двух чисел (a + b). Этот квадрат состоит из меньшего квадрата со стороной c и четырех прямоугольных треугольников с сторонами a, b и c. Давайте найдем площадь большого квадрата двумя способами:
Сначала рассчитаем площадь квадрата со стороной (a + b) как квадрат этой суммы: A = (a + b)²
Ту же самую площадь можно найти и другим способом – сложив площади всех фигур, из которых составлен квадрат: это площадь меньшего квадрата со стороной c и площади четырех треугольников. Площадь квадрата считается как c². Площадь одного прямоугольного треугольника с сторонами a, b и c найдем как половину произведения сторон a и b. Таким образом, общая площадь составит: A = c² + 4 × (ab)/2 = c² + 2ab
Поскольку оба эти расчета описывают площадь одного и того же квадрата, мы можем приравнять их друг к другу:
(a + b)² = c² + 2ab
Раскрыв квадрат суммы в левой части уравнения, получим:
a² + 2ab + b² = c² + 2ab
Отняв от обеих сторон уравнения 2ab, придем к выводу:
a² + b² = c²
Это и есть доказательство теоремы Пифагора, согласно которой в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Это объяснение показывает, как математика может быть простой и понятной, даже когда речь идет о доказательстве важных теорем. Такой подход делает математику ближе и доступнее, открывая ее красоту и логику широкому кругу людей.
Как найти стороны прямоугольного треугольника
Давайте разберем, как найти стороны прямоугольного треугольника, если известны две его стороны. Это можно сделать с помощью всем известной теоремы Пифагора. Этот способ прекрасно подходит для решения множества практических задач, будь то строительство, дизайн или даже планирование маршрутов.
Если нам известны стороны a и b прямоугольного треугольника, то длину гипотенузы c мы можем найти так: c = \sqrt{a^2 + b^2}c=a2+b2
Точно так же, если нам известны гипотенуза c и один из катетов, скажем, b, то длину другого катета a можно вычислить как: a = \sqrt{c^2 — b^2}a=c2−b2
И, наконец, если известны гипотенуза c и катет a, длину катета b найдем по формуле: b = \sqrt{c^2 — a^2}b=c2−a2
Эти формулы позволяют нам с легкостью решать задачи, связанные с прямоугольными треугольниками, используя только базовые знания математики. Таким образом, математика становится не только доступнее, но и крайне полезной в повседневной жизни и профессиональной деятельности.
Нахождение углов правильного треугольника
Давайте узнаем, как найти углы прямоугольного треугольника, если известны все три его стороны. Это довольно простая задача, если знать основы тригонометрии.
Когда у нас есть длины всех сторон треугольника, мы можем вычислить углы, не равные 90 градусам, следующим образом:
- Угол α находится напротив стороны ‘a’. Чтобы его вычислить, можно использовать одну из двух функций: arcsin(a/c) или arccos(b/c).
- Аналогично, угол β, который лежит напротив стороны ‘b’, находим через arcsin(b/c) или arccos(a/c).
Здесь ‘c’ обозначает гипотенузу треугольника, самую длинную сторону. Выбор между arcsin и arccos зависит от того, какую сторону (a или b) мы рассматриваем по отношению к углу. Используя arcsin, мы берем сторону, лежащую напротив угла, а с помощью arccos — сторону, прилегающую к углу. Оба метода корректны и позволяют точно определить величину углов в прямоугольном треугольнике.
Таким образом, зная длины сторон, мы можем не только понять, как устроен наш треугольник, но и точно определить его углы, что может пригодиться в самых разных ситуациях: от строительства до решения задач по геометрии.
Площадь прямоугольного треугольника
Чтобы вычислить площадь прямоугольного треугольника, достаточно умножить длины его катетов и разделить результат на два:
Площадь = \frac{1}{2} \times (a \times b) = \frac{a \times b}{2}Площадь=21×(a×b)=2a×b
Это означает, что если мы знаем длины двух сторон, образующих прямой угол, мы легко найдем площадь треугольника. Этот простой метод позволяет быстро решать множество задач, будь то подготовка к экзамену по геометрии или расчет материалов для строительства.
Периметр прямоугольного треугольника
Чтобы найти периметр прямоугольного треугольника, нужно просто сложить длины всех его сторон:
Периметр = a + b + c Периметр=a+b+c
Это значит, что если вы знаете длину каждой стороны треугольника, вы легко сможете вычислить общую длину его границ. Этот метод поможет вам в самых разнообразных ситуациях, от решения школьных задач по геометрии до планирования забора на даче.
Высота к гипотенузе
Если вы знаете длины всех трех сторон прямоугольного треугольника, вычислить высоту, опущенную на гипотенузу, довольно просто. Эта высота, обозначаемая как h, находится по формуле:
Высота = \frac{a \times b}{c}Высота=ca×b
Таким образом, умножив длины катетов (a и b) и разделив результат на длину гипотенузы (c), мы получим длину искомой высоты. Эта информация может пригодиться в самых разных ситуациях: от выполнения домашних заданий по математике до проектирования строительных конструкций.
Как найти гипотенузу, если известны катеты 7 и 9?
Ответ: длина гипотенузы составляет 11.40.
Для решения этой задачи используем теорему Пифагора:
Напомним формулу a^2 + b^2 = c^2a2+b2=c2, где a и b — это катеты, а c — гипотенуза. Подставляем длины катетов в формулу: 7^2 + 9^2 = c^272+92=c2. После возведения в квадрат получаем 49 + 81 = c^249+81=c2, то есть c^2 = 130c2=130. Извлекая квадратный корень, находим, что c = 11.40c=11.40. Проверить полученный результат можно с помощью онлайн-калькулятора, основанного на теореме Пифагора.
Как узнать длину катета в равнобедренном треугольнике, если гипотенуза равна 10?
Длина каждого катета составляет примерно 7.07. Давайте посмотрим, как мы пришли к этому результату, используя теорему Пифагора:
Вспоминаем формулу a^2 + b^2 = c^2a2+b2=c2, где a и b — это катеты, а c — гипотенуза. В нашем случае a = ba=b, так что формула примет вид 2a^2 = c^22a2=c2. Чтобы найти a, решаем уравнение a = c/\sqrt{2}a=c/2. Подставляя c = 10c=10, получаем ответ: a = 10/\sqrt{2} \approx 7.07a=10/2≈7.07.
Таким образом, зная длину гипотенузы, мы можем легко вычислить длину катетов в равнобедренном треугольнике, что поможет в решении множества задач, связанных с геометрией и строительством.
 Сайт с 1000 ми полезных инструментов и калькуляторов SAS Бесплатных онлайн-ресурсов с 1000+ инструментами и калькуляторами SAS. Наш сайт предлагает разнообразные сервисы, включая конструктор всплывающих окон, виджетов, визиток, генератор QR-кода, укоротитель ссылок с аналитикой, а также инструменты для скачивания видео и подбора доменных имен.
Сайт с 1000 ми полезных инструментов и калькуляторов SAS Бесплатных онлайн-ресурсов с 1000+ инструментами и калькуляторами SAS. Наш сайт предлагает разнообразные сервисы, включая конструктор всплывающих окон, виджетов, визиток, генератор QR-кода, укоротитель ссылок с аналитикой, а также инструменты для скачивания видео и подбора доменных имен. 




