Оглавление
Этот онлайн-калькулятор является незаменимым инструментом для всех, кто сталкивается с необходимостью расчета площади поверхности. Будь то профессиональные строители, дизайнеры интерьера или домашние мастера, калькулятор делает процесс вычисления простым и точным, обеспечивая результаты в различных единицах измерения, включая квадратные метры, футы, ярды и даже акры.
Простота использования данного инструмента несомненно его главное достоинство. Вам необходимо только ввести размеры интересующей поверхности, и калькулятор мгновенно предоставит точный расчет. Это идеальный инструмент для планирования расходов на строительство или ремонт, позволяя заранее узнать необходимое количество материалов.
Кроме того, калькулятор поддерживает работу с различными формами поверхностей – от простых прямоугольников до более сложных геометрических фигур, таких как трапеции и круги. Это делает его универсальным решением для расчетов в самых разных проектах.
Важным преимуществом является возможность выбора единиц измерения. В зависимости от ваших предпочтений и стандартов в вашей стране, вы можете легко переключаться между метрической и имперской системами измерения, что делает калькулятор удобным для международного использования.
Еще одна полезная функция – возможность расчета стоимости. Вводя цену за единицу площади, вы сразу получаете общую стоимость материалов для вашего проекта. Это помогает в планировании бюджета и экономии средств.
В заключение, этот калькулятор площади поверхности – незаменимый инструмент для всех, кто ищет точность, удобство и экономию времени при выполнении расчетов. Его простой интерфейс, поддержка различных форм и систем измерения делают его идеальным помощником в любом строительном или ремонтном проекте.
Инструкция по заполнению формы калькулятора площади поверхности
Заполнение формы калькулятора площади поверхности – процесс, требующий внимания к деталям. Ниже представлена пошаговая инструкция, которая поможет вам правильно использовать все функции калькулятора.
Общие сведения
Данный калькулятор предназначен для вычисления площади различных поверхностей: прямоугольников, кругов, треугольников и трапеций. Он идеален для планирования строительных и ремонтных работ, расчета материалов и бюджетирования.
Поля формы и их назначение
Длина (a), Ширина (a), Длина (b), Ширина (b), Внешний диаметр (d), Граница (w), Сторона a, Сторона b, Сторона c: В эти поля вводятся размеры измеряемой поверхности в сантиметрах или дюймах. Важно: убедитесь, что вы выбрали правильную единицу измерения.
Единицы измерения: Этот выбор позволяет переключаться между метрической и имперской системой измерения (см, м, дюймы, футы). Выбор зависит от ваших личных предпочтений или стандартов в вашей стране.
Количество: Если вам нужно рассчитать площадь нескольких одинаковых поверхностей, укажите их количество в этом поле.
Цена: Введите стоимость за единицу площади, чтобы калькулятор рассчитал общую стоимость материалов.
Как правильно заполнять
При измерении длины и ширины вашей поверхности используйте рулетку. Если размеры в метрах, укажите их в поле с метрической системой. Например, для длины 2 метра введите «200» в поле см.
При работе с круглыми формами, в поле «Диаметр (d)» введите полный размер через центр круга. Для круга диаметром 1 метр введите «100» см.
В поле «Единицы измерения» выберите нужную опцию из списка. Это определит, в каких единицах будут выведены результаты.
«Количество» позволяет умножить полученную площадь на указанное число поверхностей. Это полезно, когда нужно рассчитать одинаковые элементы, например, плитку для пола.
Вводя цену, не забывайте про единицу измерения. Если цена указана за квадратный метр, убедитесь, что выбрана соответствующая опция.
Важные моменты
- Всегда проверяйте, в какой системе измерения (метрической или имперской) вы собираетесь вводить данные.
- Помните, что переключение между вкладками (прямоугольник, круг, треугольник) изменяет набор полей для заполнения.
- Для точности расчетов измеряйте все размеры как можно точнее.
- Перед тем как нажать «Рассчитать площадь», убедитесь, что все поля заполнены корректно.
Следуя этой инструкции, вы сможете максимально точно и эффективно использовать калькулятор для расчета площади поверхности. Это поможет вам в планировании и оптимизации расходов на материалы.
Серия примеров использования калькулятора площади поверхности
Эти примеры демонстрируют, как калькулятор площади поверхности может быть использован для решения разнообразных практических задач, от строительства и ремонта до ландшафтного дизайна.
Расчет площади комнаты для покраски
Задача: Вы хотите покрасить стены в комнате размером 5 метров в длину и 4 метра в ширину. Какова площадь стен, которую нужно покрасить?
Шаги решения:
- Выберите вкладку «Прямоугольник».
- Введите длину комнаты (5 м) и ширину комнаты (4 м) в соответствующие поля.
- Учитывая, что высота потолков стандартная (около 2.5 м), умножьте периметр комнаты на высоту потолка, чтобы получить общую площадь стен.
- Нажмите «Рассчитать площадь».
Результаты расчета: Периметр комнаты равен (5+4) \times 2 = 18(5+4)×2=18 м. Площадь стен для покраски составит 18 \times 2.5 = 4518×2.5=45 квадратных метров.
Применение на практике: Зная площадь, вы можете рассчитать количество краски, необходимое для покраски комнаты, исходя из рекомендаций производителя краски на упаковке.
Вычисление необходимого количества плитки для ванной
Задача: Вам нужно выложить плиткой стены в ванной комнате размером 2 на 3 метра и высотой 2.5 метра.
Шаги решения:
- Выберите вкладку «Прямоугольник».
- Введите размеры стен: длину (2 м), ширину (3 м) и высоту (2.5 м).
- Рассчитайте периметр комнаты и умножьте его на высоту, чтобы получить общую площадь стен.
- Нажмите «Рассчитать площадь».
Результаты расчета: Периметр ванной составляет (2+3) \times 2 = 10(2+3)×2=10 м. Площадь стен равна 10 \times 2.5 = 2510×2.5=25 квадратных метров.
Применение на практике: Зная общую площадь, вы можете определить количество плитки, необходимое для отделки стен в ванной, учитывая размер выбранной вами плитки.
Определение количества семян травы для газона
Задача: Вы планируете посеять траву на круглом газоне диаметром 10 метров. Сколько семян травы вам понадобится, если известно, что на один квадратный метр требуется 30 г семян?
Шаги решения:
- Выберите вкладку «Круг».
- Введите диаметр газона (10 м) в соответствующее поле.
- Нажмите «Рассчитать площадь».
Результаты расчета: Площадь круглого газона равна \pi \times (10/2)^2 \approx 78.54π×(10/2)2≈78.54 квадратных метров.
Применение на практике: Для посева травы на газоне площадью 78.54 кв. м потребуется 78.54 \times 30 = 2356.278.54×30=2356.2 грамм семян травы.
Таблица руководство по выбору единиц измерения для различных задач
Эта таблица поможет выбрать подходящие единицы измерения в зависимости от ваших задач и упростит работу с калькулятором площади поверхности.
| Задача/Проект | Единица измерения | Почему именно эта единица? | Пример применения |
|---|---|---|---|
| Покраска стен | квадратные метры (м²) | Удобно для расчета объема краски в большинстве стран | Рассчитать, сколько краски нужно для стен комнаты |
| Укладка плитки | квадратные метры (м²) | Стандартная единица для площади полов и стен | Определить количество плитки для ванной комнаты |
| Садовые работы | квадратные метры (м²) или акры | Для больших участков удобнее использовать акры | Планирование посадочных площадей на участке |
| Строительство | квадратные метры (м²) или квадратные футы (ft²) | В зависимости от страны и предпочтений | Расчет площади для заливки фундамента |
| Изготовление мебели | квадратные сантиметры (см²) | Точность важна при работе с небольшими деталями | Расчет материала для столешницы |
| Планирование полива | квадратные метры (м²) | Удобно для расчета системы полива | Расчет необходимости воды для газона |
| Ремонт крыши | квадратные метры (м²) или квадратные футы (ft²) | В зависимости от страны и размеров крыши | Определение количества кровельного материала |
Как пользоваться таблицей:
- Определите свою задачу или проект из первого столбца.
- Выберите рекомендуемую единицу измерения.
- Учитывайте, почему именно эта единица предпочтительна для вашей задачи, это поможет вам в планировании.
- Используйте пример применения как ориентир для своих расчетов.
Эта таблица станет вашим надежным помощником при работе с калькулятором площади поверхности, позволяя выбрать наиболее подходящие единицы измерения для различных видов работ и проектов.
Что такое площадь поверхности? Простое объяснение
Площадь поверхности — это весь размер, который занимает поверхность объекта. Если говорить проще, это общий размер всех сторон трехмерного предмета.
Иногда площадь поверхности можно разделить на две части: площадь основания(ий) и площадь боковой поверхности. Боковая поверхность — это размер всех сторон объекта, кроме его основания и верха. Такое разделение удобно использовать для фигур, где четко видно разницу между основанием и остальными частями. Например, это актуально для цилиндра, конуса, пирамиды или треугольной призмы. Для тел с неопределенными гранями, как куб или коробка, этот метод не используют. Также его не применяют к объектам с гладкими поверхностями, типа сферы.
Это знание особенно полезно, когда вам нужно вычислить, сколько материала потребуется для покрытия объекта. Например, это может быть краска для стен вашего дома или оберточная бумага для подарка необычной формы. Понимая, что такое площадь поверхности и как ее рассчитать, вы сможете более точно планировать необходимые ресурсы для своих проектов или задач.
Как рассчитать площадь поверхности разных тел?
Наши инструменты позволяют вычислить площадь поверхности семи различных геометрических тел. В зависимости от формы тела используются разные формулы.
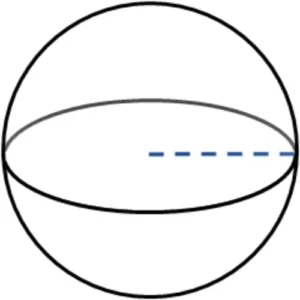
Сфера
Площадь поверхности сферы можно найти по формуле: A = 4πr², где r — это радиус сферы.
Куб
Для куба формула площади поверхности выглядит как A = 6a², где a — длина стороны куба.
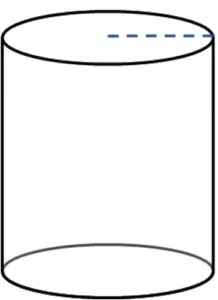
Цилиндр
Площадь цилиндра рассчитывается так: A = 2πr² + 2πrh, где r — радиус основания, а h — высота цилиндра.
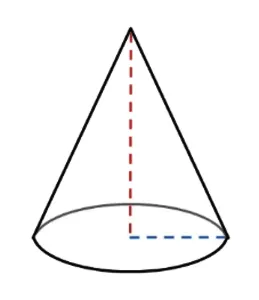
Конус
Чтобы узнать площадь поверхности конуса, используйте A = πr² + πr√(r² + h²), где r — радиус основания, а h — высота конуса.
Прямоугольный параллелепипед (Коробка)
Для него формула выглядит так: A = 2(ab + bc + ac), где a, b, c — длины трех сторон параллелепипеда.
Треугольная призма
Площадь треугольной призмы находят по формуле: A = 0.5 × √((a + b + c) × (-a + b + c) × (a — b + c) × (a + b — c)) + h × (a + b + c), где a, b, c — длины сторон основания призмы, а h — высота (длина) призмы.
Пирамида
Площадь поверхности пирамиды рассчитывается как A = l × √(l² + 4 × h²) + l², где l — длина стороны квадратного основания, а h — высота пирамиды.
Эти формулы помогут вам легко определить площадь поверхности, нужную для решения широкого круга задач: от строительства и дизайна до научных расчетов. Использование правильной формулы гарантирует точность ваших вычислений, обеспечивая успешное выполнение проектов и экономию материалов.
Как рассчитать площадь поверхности шара?
Чтобы вычислить площадь поверхности шара, вам всего лишь нужно знать радиус шара или его диаметр.
Формула выглядит так: A = 4 × π × r², где r — радиус шара. Учитывая, что диаметр шара в два раза больше его радиуса (d = 2r), мы можем переписать формулу в другом виде:
A = 4 × π × (d / 2)² = π × d², где d — диаметр шара.
Получение этой формулы площади поверхности требует знаний в области интегрирования. Если вам интересно узнать, как она выводится, можно посмотреть соответствующее доказательство.
Эта информация будет полезна не только для решения задач по геометрии, но и в практических ситуациях, например, когда нужно окрасить шаровую конструкцию или рассчитать материал для её покрытия. Зная радиус или диаметр шара, вы легко сможете определить его площадь поверхности, что поможет вам точно спланировать необходимое количество материалов.
Как посчитать площадь поверхности цилиндра?
Чтобы вычислить площадь поверхности цилиндра, вам нужно знать две вещи: радиус (или диаметр) основания и высоту цилиндра. Общая формула состоит из суммы площадей оснований и площади боковой поверхности. В нашем случае основанием служит круг.
Формула выглядит так: A = 2πr² + 2πrh, где r — радиус основания, а h — высота цилиндра.
Откуда берется эта формула? Площадь поверхности цилиндра можно представить как сумму площади боковой поверхности и удвоенной площади основания. Площадь основания легко найти, вспомнив известную формулу площади круга: A(основание) = π × r². А как выглядит боковая поверхность? Попробуйте представить, что вы «развернули» ее. Узнаете? Это прямоугольник! Одна из сторон прямоугольника — это высота цилиндра, а вторая — длина окружности основания.
Таким образом, расчет площади поверхности цилиндра становится понятным и доступным даже для тех, кто далек от математики. Эти знания могут пригодиться в различных ситуациях: от школьных задач до практических расчетов в проектах, связанных со строительством или дизайном.
Как найти площадь поверхности конуса?
Площадь поверхности конуса можно разделить на две части: боковую поверхность и основание. В отличие от цилиндра, у конуса только одно основание.
Основание конуса — это круг с площадью A(основание) = π × r², где r — радиус основания. Определение боковой площади может показаться сложным, но на самом деле всё логично:
A(боковая) = π × r × √(r² + h²)
Давайте разберёмся, как это работает шаг за шагом:
Развертка боковой поверхности. Если мысленно развернуть боковую поверхность конуса, получится сектор круга, радиус которого (s) равен образующей конуса.
Длина окружности большого круга с радиусом s будет 2 × π × s. Длина дуги сектора равна 2 × π × r.
Площадь сектора (наша боковая поверхность конуса) вычисляется по формуле: A(боковая) = π × r × s.
Эту формулу можно получить из соотношения площадей и длин окружностей. Поскольку обычно мы знаем высоту (h) конуса, а не образующую (s), используем теорему Пифагора для преобразования формулы: √(r² + h²) = s.
Таким образом, формула для боковой поверхности принимает вид:
A(боковая) = π × r × √(r² + h²)
Наконец, чтобы найти полную площадь поверхности конуса, нужно сложить площади основания и боковой части:
A = A(боковая) + A(основание) = π × r × √(r² + h²) + π × r²
Такой подход к расчету площади поверхности конуса позволяет легко определить, сколько материала потребуется для его создания или декорирования, будь то ткань для платья в виде конуса или бумага для поделки.
Как рассчитать площадь поверхности куба?
Площадь поверхности куба — это, пожалуй, одна из самых простых вещей, которые только можно себе представить. Каждая из его граней — это квадрат. Поскольку у куба шесть одинаковых квадратных граней, общая площадь поверхности складывается из площадей всех этих граней:
A = 6 × (площадь одной грани)
Так как площадь квадрата равна произведению длин его сторон, итоговая формула для вычисления площади поверхности куба выглядит так:
A = 6 × l², где l — длина стороны квадрата.
Эта простая формула может пригодиться в самых разных ситуациях. Например, если вы хотите покрасить кубическую коробку или упаковать её в подарочную бумагу, знание площади поверхности поможет вам точно определить, сколько краски или бумаги потребуется. Также это знание полезно в области строительства, дизайна и многих других сферах, где важно знать размеры поверхностей.
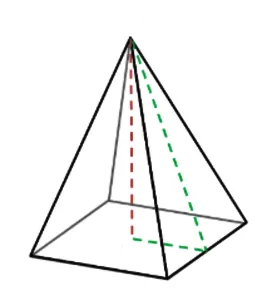
Как рассчитать площадь поверхности пирамиды
Пирамида — это трехмерное тело с многоугольным основанием и треугольными боковыми гранями. Когда мы говорим о пирамиде, чаще всего представляем себе пирамиду с квадратным основанием. Но в зависимости от формы основания, она может быть также шестиугольной или прямоугольной. Под словом «регулярная» подразумевается пирамида с правильным многоугольником в основании и вершиной, строго над центром основания. «Квадратная» означает, что основание имеет форму квадрата. Именно такую пирамиду мы используем для расчетов в нашем калькуляторе площади поверхности.
Формула для расчета площади поверхности пирамиды выглядит так:
A = l × √(l² + 4 × h²) + l², где l — длина стороны основания, а h — высота пирамиды.
Разделим уравнение на две части:
A = A(основание) + A(боковая) = l² + 4 × A(боковая грань)
Основание пирамиды представляет собой квадрат, поэтому A(основание) = l². Для расчета боковой площади начнем с площади одной треугольной грани:
Для нахождения высоты треугольника нам понадобится формула гипотенузы:
c = √(a² + b²)
Вычислим гипотенузу треугольника ABC (которая одновременно является высотой треугольной грани):
c = √(h² + (l/2)²) = √(h² + l²/4)
Площадь треугольника (в нашем случае это равнобедренный треугольник) можно рассчитать как:
A = высота × основание / 2, так что
A(боковая грань) = √(h² + l²/4) × l / 2
Итак, окончательная формула для площади поверхности пирамиды:
A = l² + 4 × √(h² + l²/4) × l / 2 = l² + 2 × l × √(h² + l²/4)
A = l² + l × √(4 × h² + l²)
Эта формула поможет вам легко рассчитать необходимое количество материалов для покрытия пирамиды или её модели, будь то в строительстве, дизайне или образовательных проектах.
Как рассчитать площадь поверхности прямоугольного параллелепипеда?
Чтобы узнать, какова площадь поверхности обычной коробки или прямоугольного параллелепипеда, вам просто нужно посчитать площади всех его прямоугольных сторон.
Формула для этого довольно проста:
A = 2 × (A1 + A2 + A3)
Здесь:
- A1 это площадь одной из сторон, которую мы находим, умножая его длину (l) на ширину (w).
- A2 — это площадь второй стороны, получаемая умножением ширины (w) на высоту (h).
- A3 — площадь третьей стороны, вычисляемая умножением длины (l) на высоту (h).
Итак, окончательная формула выглядит так:
A = 2 × (l × w + w × h + l × h)
Эта формула поможет вам легко рассчитать, сколько материала потребуется для обшивки, покраски или обертывания прямоугольного параллелепипеда. Она особенно полезна, если вы занимаетесь строительством, декором или просто хотите упаковать в подарок большую коробку. Понимание этой простой математической операции позволит вам точно спланировать количество необходимых материалов без лишних затрат.
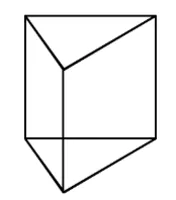
Как вычислить площадь поверхности треугольной призмы?
Чтобы понять, как появляется формула для расчета площади поверхности треугольной призмы, давайте рассмотрим это пошагово:
Боковая поверхность призмы рассчитывается довольно просто. Как видно из иллюстрации, она состоит из трех прямоугольников, у каждого из которых одна сторона совпадает:
A(боковая) = a × h + b × h + c × h = h × (a + b + c)
Это можно записать в сокращенном виде как:
A(боковая) = h × P, где P — это периметр одного из оснований в виде треугольника.
Затем находим площадь одного из треугольных оснований. Это можно сделать разными способами, в зависимости от имеющихся данных. В нашем калькуляторе используется формула Герона — она применяется, когда известны длины всех трех сторон треугольника:
A(основание) = 0.25 × √((a + b + c) × (-a + b + c) × (a — b + c) × (a + b — c))
Окончательная формула для площади поверхности треугольной призмы выглядит так:
A = A(боковая) + 2 × A(основание)
A = h × (a + b + c) + 0.5 × √((a + b + c) × (-a + b + c) × (a — b + c) × (a + b — c))
Это объяснение поможет вам легко вычислить необходимую площадь для обшивки, декорирования или покраски треугольной призмы, будь то игрушка, элемент декора или конструкционная деталь в строительстве. Знание этих формул облегчит планирование и поможет избежать лишних трат материалов.
Как найти длину стороны куба, зная площадь поверхности?
Если перед вами стоит задача вычислить длину стороны куба, зная его общую площадь поверхности, действуйте по следующему плану:
- Запишите общую площадь поверхности вашего куба.
- Разделите эту площадь на шесть. Полученное число будет площадью одной из граней куба.
- Извлеките квадратный корень из числа, полученного на втором шаге.
- Полученный результат и будет искомой длиной стороны куба. Отличная работа!
Этот метод позволяет легко перейти от общей площади поверхности к размеру стороны куба, что может быть полезно в решении задач по геометрии, в строительстве, дизайне или при работе с материалами. Такой подход делает математику понятной и доступной.
Как определить радиус шара, зная площадь поверхности?
Если вам известна площадь поверхности шара и требуется найти его радиус, просто следуйте этим шагам:
- Запишите площадь поверхности шара.
- Разделите эту площадь на 4π (примерно равно 12.566).
- Извлеките квадратный корень из полученного частного: √(Площадь / 4π).
- Вот и все, перед вами радиус шара! Для проверки полученного результата можно воспользоваться онлайн-калькулятором площади поверхности.
Этот метод позволяет без труда перейти от общей площади поверхности к радиусу шара, что особенно полезно в задачах по геометрии, физике или при планировании материалов для сферических объектов. Такой подход делает математические расчеты доступными и понятными.
Как найти площадь поверхности цилиндра с радиусом и высотой 2 дюйма?
Если перед вами стоит задача вычисления площади поверхности цилиндра, у которого радиус и высота равны 2 дюймам, ответ будет 50.2655 квадратных дюймов. Для нахождения этого результата вспомним формулу площади поверхности цилиндра:
Площадь = 2πr(r + h)
Подставив значения r = h = 2, получаем Площадь = 16π ≈ 50.2655. Не забывайте про единицы измерения! Поскольку и радиус, и высота указаны в дюймах, площадь выражается в квадратных дюймах.
Этот метод расчета позволяет легко определить необходимое количество материала для покрытия цилиндрической поверхности или для других практических нужд, связанных с цилиндрами. Понимание таких основ геометрии делает решение повседневных задач более доступным и понятным.
Стереометрия
Куб
- Диагональ d = \sqrt{3}ad=3a
- Площадь полной поверхности S_{п.п.} = 6a^2Sп.п.=6a2
- Объем V = a^3V=a3
Прямоугольный параллелепипед
- Диагональ d = \sqrt{a^2 + b^2 + c^2}d=a2+b2+c2
- Площадь полной поверхности S_{п.п.} = 2c (a + b)Sп.п.=2c(a+b)
- Объем V = abcV=abc
- Площадь полной поверхности S_{п.п.} = 2(ac + bc + ab)Sп.п.=2(ac+bc+ab)
Призма
- Площадь боковой поверхности S_{б.п.} = P_{осн.} \cdot HSб.п.=Pосн.⋅H
- Площадь боковой поверхности S_{б.п.} = P_{осн.} \cdot lSб.п.=Pосн.⋅l, где ll — апофема перпендикулярного сечения
- Площадь полной поверхности S_{п.п.} = 2S_{осн.} + S_{б.п.}Sп.п.=2Sосн.+Sб.п.
- Объем V = S_{осн.} \cdot HV=Sосн.⋅H
Правильная пирамида
- Площадь боковой поверхности S_{б.п.} = \frac{1}{2}plSб.п.=21pl
- Объем V = \frac{1}{3}S_{осн.}HV=31Sосн.H
Цилиндр
- Площадь боковой поверхности S_{б.п.} = 2\pi RHSб.п.=2πRH
- Объем V = \pi R^2HV=πR2H
- Площадь полной поверхности S_{п.п.} = \pi R (R + H)Sп.п.=πR(R+H)
Шар
- Площадь поверхности S = 4\pi R^2 = \pi d^2S=4πR2=πd2
- Объем V = \frac{4}{3}\pi R^3 = \frac{1}{6}\pi d^3V=34πR3=61πd3
Конус
- Площадь боковой поверхности S_{б.п.} = \pi rlSб.п.=πrl
- Площадь полной поверхности S_{п.п.} = \pi R (R + l)Sп.п.=πR(R+l)
- Объем V = \frac{1}{3}\pi R^2HV=31πR2H
Усеченный конус
- Площадь боковой поверхности S_{б.п.} = \pi (R + r)lSб.п.=π(R+r)l
- Площадь полной поверхности S_{п.п.} = S_{б.п.} + \pi (R^2 + r^2)Sп.п.=Sб.п.+π(R2+r2)
- Объем V = \frac{1}{3}\pi H (R^2 + Rr + r^2)V=31πH(R2+Rr+r2)
Шаровой сектор
- Площадь боковой поверхности S_{б.п.} = 2\pi R hSб.п.=2πRh
- Объем V = \frac{2}{3}\pi R^2hV=32πR2h
Шаровой сегмент
- Площадь боковой поверхности S_{б.п.} = 2\pi RhSб.п.=2πRh
- Объем V = \frac{\pi h}{6} (3R^2 + h^2)V=6πh(3R2+h2)
Обратите внимание, что в формулах использованы символы:
- a, b, ca,b,c — ребра параллелепипеда и куба,
- dd — диагональ куба или параллелепипеда,
- S_{п.п.}Sп.п. — площадь полной поверхности,
- S_{б.п.}Sб.п. — площадь боковой поверхности,
- VV — объем,
- RR и rr — радиусы оснований цилиндра, конуса, шара,
- HH — высота,
- ll — апофема или образующая,
- hh — высота сегмента или сектора шара,
- P_{осн.}Pосн. — периметр основания призмы или пирамиды.
 Сайт с 1000 ми полезных инструментов и калькуляторов SAS Бесплатных онлайн-ресурсов с 1000+ инструментами и калькуляторами SAS. Наш сайт предлагает разнообразные сервисы, включая конструктор всплывающих окон, виджетов, визиток, генератор QR-кода, укоротитель ссылок с аналитикой, а также инструменты для скачивания видео и подбора доменных имен.
Сайт с 1000 ми полезных инструментов и калькуляторов SAS Бесплатных онлайн-ресурсов с 1000+ инструментами и калькуляторами SAS. Наш сайт предлагает разнообразные сервисы, включая конструктор всплывающих окон, виджетов, визиток, генератор QR-кода, укоротитель ссылок с аналитикой, а также инструменты для скачивания видео и подбора доменных имен.