Калькулятор соотношения

Упрощение и сравнение соотношений чисел базируются на двух важных математических концепциях: наименьшем общем кратном (НОК) и наибольшем общем делителе (НОД). Давайте разберемся с этими понятиями:

1. Наибольший общий делитель (НОД):

   • НОД двух чисел — это наибольшее число, которое делит оба числа без остатка.
   • НОД играет важную роль в упрощении соотношений чисел. Если числитель и знаменатель можно оба поделить на НОД, то соотношение будет упрощено до наименьших целых чисел.
   • Например, для соотношения 6/8 НОД чисел 6 и 8 равен 2. Если мы поделим и числитель, и знаменатель на 2, получим упрощенное соотношение 3/4.

2. Наименьшее общее кратное (НОК):

   • НОК двух чисел — это наименьшее число, которое является кратным обоим числам.
   • НОК часто используется при сравнении разных дробей, чтобы привести их к общему знаменателю.
   • Например, для сравнения 2/5 и 3/7, мы можем найти НОК знаменателей 5 и 7, который равен 35. Затем привести обе дроби к общему знаменателю: 2/5 * 7/7 = 14/35 и 3/7 * 5/5 = 15/35.

Таким образом, математические основы упрощения и сравнения соотношений чисел заключаются в использовании НОД и НОК. НОД помогает упростить соотношение путем деления числителя и знаменателя на их общий делитель, а НОК позволяет сравнивать дроби, приводя их к общему знаменателю. Эти концепции играют важную роль в различных математических задачах и при работе с долями и пропорциями.

Округление результатов при работе с десятичными числами — это важный аспект, который может влиять на точность и понимание данных. Вот несколько методов округления и советов по их выбору:

1. Округление до заданного числа десятичных знаков:

   • Этот метод применяется, когда требуется ограничить количество десятичных знаков в результате. Например, округлите число 3.45678 до двух десятичных знаков: 3.46.
   • При этом методе необходимо учитывать последний округляемый знак. Если он больше или равен 5, то следующий знак округляется в большую сторону, иначе в меньшую.

2. Округление до целого числа:

   • В этом случае результат округляется до ближайшего целого числа. Например, округлите число 3.8 до ближайшего целого: 4.
   • Если дробная часть равна или больше 0.5, то число округляется в большую сторону, иначе — в меньшую.

3. Округление в меньшую сторону (отсечение дробной части):

   • Этот метод используется, когда необходимо убрать дробную часть и оставить только целое число. Например, 3.8 округляется в 3.
   • Важно помнить, что при таком округлении всегда удаляется дробная часть, даже если она больше 0.5.

4. Округление в большую сторону (округление вверх):

   • Этот метод применяется, когда необходимо гарантировать, что число округляется в большую сторону. Например, 3.2 округляется до 4.
   • Важно понимать, что даже если дробная часть меньше 0.5, число все равно округляется в большую сторону.

5. Банковское округление (округление к ближайшему «четному» числу):

   • Этот метод используется, чтобы уменьшить систематическую ошибку при округлении большого набора чисел. При этом дробные числа, оканчивающиеся на 0.5, округляются к ближайшему четному целому числу. Например, 2.5 округляется до 2, а 3.5 — до 4.

Выбор метода округления зависит от конкретной задачи и требований к точности. Важно учитывать, какой результат будет наиболее релевантным и понятным в контексте вашей работы. Также стоит помнить о стандартах округления, которые могут быть установлены в вашей области, таких как банковское округление в финансовых расчетах.

1. Наибольший общий делитель (НОД):

   • Определение: НОД двух или более чисел — это наибольшее число, которое делит каждое из этих чисел без остатка. Иными словами, это самое большое общее число, которое является делителем для всех заданных чисел.

2. Наименьшее общее кратное (НОК):

   • Определение: НОК двух или более чисел — это наименьшее положительное число, которое является кратным каждому из этих чисел. Иными словами, это наименьшее общее кратное, которое делится без остатка на все заданные числа.

3. Упрощение:

   • Определение: Упрощение числового соотношения — это процесс приведения его к более простому виду путем деления числителя и знаменателя на их общий делитель. Это позволяет представить соотношение в более компактной и удобной форме, сохраняя его эквивалентность.

4. Соотношение чисел:

   • Определение: Соотношение чисел представляет собой отношение между двумя числами, выраженное в виде дроби, где числитель — это число, которое мы рассматриваем, а знаменатель — это число, относительно которого мы его измеряем.

5. Округление:

   • Определение: Округление числа — это процесс приближения числа до другого числа с меньшим количеством десятичных знаков. Это делается для упрощения вычислений и представления чисел в более удобной форме.

6. Банковское округление:

   • Определение: Банковское округление — это метод округления чисел, при котором дробные числа, оканчивающиеся на 0.5, округляются до ближайшего четного целого числа. Например, 2.5 округляется до 2, а 3.5 — до 4. Этот метод используется в финансовых расчетах для уменьшения систематических ошибок.

Эти определения помогут пользователям понять ключевые математические концепции, связанные с соотношениями чисел, округлением и другими аспектами работы с числами.

Соотношение в математике представляет собой способ сравнения двух чисел или величин одной и той же единицы измерения, чтобы определить, как одно число связано с другим. Соотношение обычно записывается в виде двух чисел, разделенных двоеточием. Например, соотношение 7:10, о котором вы упомянули, представляет собой отношение между количеством полученных баллов (7) и общим количеством баллов (10).

Соотношения могут использоваться для описания различных отношений или сравнений в математике и в реальной жизни. Они могут быть использованы для выражения процентов, долей, отношений частей к целому и многих других математических и практических концепций.

Важно понимать, что соотношение может быть представлено в различных формах и может быть упрощено до более простых видов для удобства анализа и сравнения.

Соотношение может быть записано несколькими способами:

1. Использование двоеточия (:): В этом случае, два числа или величины разделяются двоеточием. Например, если у нас есть соотношение яблок к дыням, где 4 яблока и 8 дынь, то соотношение можно записать как «4:8». Это показывает, что на каждые 4 яблока приходится 8 дынь.

2. Использование дробей: Соотношение также можно записать в виде дроби, где числитель представляет одну величину, а знаменатель — другую величину. В примере с яблоками и дынями, соотношение можно записать как «4/8». Затем эту дробь можно упростить, деля как числитель, так и знаменатель на общий делитель (в данном случае, на 4), и получить упрощенное соотношение «1/2».

Оба способа записи соотношения (с помощью двоеточия и дроби) являются корректными и могут быть удобными в разных ситуациях в зависимости от контекста и целей.

Для расчета соотношения между двумя числами можно использовать следующие шаги:

Пример: Для приготовления крема для глазури необходимо 14 чашек сливочного масла и 28 чашек сахара. Каково соотношение масла и сахара?

Шаг 1: Обратите внимание на количество обоих ингредиентов, для которых вы определяете соотношение. В данном случае это 14 и 28.

Шаг 2: Запишите это в форме дроби a/b. Таким образом, мы записываем это как 14/28.

Шаг 3: Упростите дробь, если это возможно. Для этого найдите наибольший общий коэффициент (НОК) между числами 14 и 28. НОК равен 14, поэтому разделим оба числа на 14:

(14 ÷ 14) / (28 ÷ 14) = 1/2.

Шаг 4: Таким образом, соотношение масла к сахару упрощается до 1:2.

Ответ: Соотношение масла к сахару в глазуре составляет 1:2. Это означает, что для каждой части сливочного масла используется две части сахара при приготовлении.

Для нахождения эквивалентных соотношений вы можете использовать операции умножения или деления. Эквивалентные соотношения представляют одно и то же отношение между двумя величинами, но могут быть записаны в разных числовых выражениях. Давайте рассмотрим примеры:

Пример 1: Эквивалентные соотношения с помощью умножения.

Допустим, у нас есть исходное соотношение 1:4. Мы хотим найти эквивалентное соотношение, умножив оба члена на 2.

• Исходное соотношение: 1:4
• Умножим оба члена на 2: (1 * 2) : (4 * 2) = 2:8

Теперь 1:4 и 2:8 являются эквивалентными соотношениями, так как они представляют одно и то же отношение.

Пример 2: Эквивалентные соотношения с помощью деления.

Допустим, у нас есть исходное соотношение 30:10. Мы хотим найти эквивалентное соотношение, разделив оба члена на 10.

• Исходное соотношение: 30:10
• Разделим оба члена на 10: (30 ÷ 10) : (10 ÷ 10) = 3:1

Теперь 30:10 и 3:1 являются эквивалентными соотношениями.

Эквивалентные соотношения могут быть найдены путем умножения или деления обоих членов исходного соотношения на одно и то же число, отличное от нуля. Это позволяет представить одно и то же отношение в разных числовых форматах для удобства сравнения и анализа.

Таблица коэффициентов представляет собой структурированный список эквивалентных соотношений, получаемых путем умножения или деления обоих членов исходного соотношения на одно и то же значение (обычно целое число). Эта таблица служит для наглядного представления различных числовых форм соотношения, которые представляют одно и то же отношение.

Пример:

• Начальное соотношение: 1:3
• При умножении обоих членов на 2 получается: 2:6
• При умножении обоих членов на 3 получается: 3:9
• При умножении обоих членов на 4 получается: 4:12

И так далее…

Когда эти соотношения упрощаются, они представляют одно и то же значение, как в случае с вашим примером, где все они упрощаются до 1:3. То есть, хотя числовые значения в соотношениях разные, суть отношения остается неизменной.

Таблицы коэффициентов могут быть полезными инструментами для анализа и сравнения различных числовых выражений, представляющих одно и то же отношение, а также для иллюстрации принципа эквивалентных соотношений.

Коэффициенты и соотношения играют важную роль в различных аспектах математики и реального мира по следующим причинам:

1. Сравнение и анализ: Коэффициенты и соотношения позволяют сравнивать размеры или количества двух или более величин. Они делают числа более интерпретируемыми, позволяя нам легко определить, как одно число связано с другим.

2. Упрощение: Коэффициенты и соотношения могут быть упрощены до более простых форм, что облегчает их анализ и сравнение. Упрощенные формы могут быть более наглядными и понятными.

3. Масштабирование: Коэффициенты позволяют масштабировать величины. Например, если у нас есть соотношение 1:3, мы можем умножить оба члена на 10 и получить новое соотношение 10:30. Это помогает анализировать данные на разных уровнях масштаба.

4. Понимание отношений: Соотношения помогают выразить отношения между разными группами или категориями данных. Они могут использоваться для описания процентов, долей, соотношений частей к целому и других важных концепций.

5. Решение задач: В реальной жизни соотношения часто используются для решения задач, связанных с распределением ресурсов, планированием, финансами и другими областями. Например, при бюджетировании можно использовать соотношения для определения распределения средств на различные категории.

Важно уметь работать с коэффициентами и соотношениями, так как они являются мощным инструментом для анализа данных и принятия решений в различных областях, включая математику, статистику, финансы и научные исследования.

Формула соотношения используется для представления отношения между двумя величинами или числами и выглядит следующим образом:

a : b

где:

• «a» представляет собой первую величину или число.
• «b» представляет собой вторую величину или число.

Эта формула используется для указания того, как одна величина связана с другой величиной. Символ «:» читается как «к», и он обозначает отношение между «a» и «b». Такое представление позволяет легче понимать, насколько одна величина больше или меньше другой и как они связаны друг с другом.

Например, если у нас есть соотношение 3 : 4, это означает, что первая величина (3) встречается в отношении к второй величине (4) так, что она встречается 3 раза в то время, как вторая встречается 4 раза. Эта форма представления широко используется для сравнения и анализа данных в различных областях, включая математику, статистику и науку.

Соотношение и пропорция — это важные концепции в математике, связанные с сравнением величин.

Соотношение — представляет собой сравнение между двумя величинами или числами одной и той же единицы измерения. Оно используется для определения, насколько одна величина больше или меньше другой. Соотношение записывается как a/b или a: b, где «a» и «b» — это числа или величины, и «b» не равно нулю. Например, соотношение 3:2 говорит нам, что первая величина (3) встречается в отношении ко второй величины (2) так, что она больше второй.

Пропорция — это равенство двух соотношений. Пропорции используются для установления эквивалентных отношений между разными наборами чисел или величин. Пропорция записывается как a:b = c:d, где «a», «b», «c» и «d» — это числа или величины. Когда пропорция верна, это означает, что отношение между «a» и «b» такое же, как отношение между «c» и «d». Пропорции могут быть использованы для решения задач, связанных с неизвестными величинами. Например, если вы знаете, что a:b = 2:3 и c:a = 4:5, вы можете использовать пропорцию, чтобы найти значение «c» в отношении к «b».

Пропорции и соотношения широко применяются в математике, физике, экономике и других научных и инженерных областях для анализа и решения различных задач.

Сравнение коэффициентов, представленных в виде соотношений, можно выполнить с использованием различных методов.

1. Общие знаменатели: Если знаменатели в соотношениях уже общие (или легко сделать их общими), то можно сравнить числители напрямую. Например, сравнивая 1/2 и 2/3, можно заметить, что знаменатели могут быть сделаны общими, и тогда сравниваются числители 1 и 2.

2. Перевод в десятичные дроби: Можно преобразовать оба соотношения в десятичные дроби, а затем сравнить их числительные значения. Например, 1/2 в десятичном виде равно 0,5, а 2/3 в десятичном виде равно приближенно 0,6667. Тогда можно сказать, что 2/3 больше, чем 1/2.

3. Сравнение отношений числителей и знаменателей: Вы можете также сравнивать отношения числителей к знаменателям в каждом соотношении. Например, в 1/2 отношение числителя (1) к знаменателю (2) равно 1:2, а в 2/3 отношение числителя (2) к знаменателю (3) равно 2:3. Затем можно сравнить эти отношения.

4. Графическое представление: В некоторых случаях можно построить график для каждого соотношения на числовой оси и визуально сравнить их положение относительно друг друга.

Выбор метода зависит от конкретной ситуации и того, какие данные у вас есть.

Преобразование соотношения в дробь очень просто выполняется, предшествующее число записывается как числитель, а последующее число записывается как знаменатель.

Например, если дано соотношение 3:5, где 3 — предшествующее число, а 5 — последующее, то мы можем записать его в виде дроби как 3/5. Это представляет соотношение в дробном виде, где 3 — числитель, а 5 — знаменатель.

Применение этого простого правила позволяет легко преобразовывать соотношения в дроби для анализа и сравнения величин.

Сначала дробь упрощается до её наименьших членов, а затем записывается в виде соотношения, где числитель становится предшествующим членом, а знаменатель — последующим.

Для преобразования дроби 16/48 в соотношение, мы сначала упростим эту дробь до 1/3, затем представим её в виде соотношения как 1:3. Это означает, что соотношение числа 1 к числу 3 показывает тот же самый относительный размер, что и изначальная дробь 16/48.

Для этого сначала соотношение записывается в виде дроби, где предшествующее число становится числителем, а последующее — знаменателем. Например, соотношение 3:7 записывается как 3/7.

Затем, чтобы получить десятичную дробь, числитель дроби (в данном случае, 3) делится на знаменатель (7). Это даёт результат в виде десятичной дроби. В вашем примере, 3/7 примерно равно 0,4285714 и так далее, но в обычной практике обычно округляется до нужного количества десятичных знаков.

Преобразование коэффициентов в проценты действительно выполняется путем преобразования соотношения в дробь, а затем умножения этой дроби на 100 и добавления символа процента.

Например, если у вас есть соотношение 5:6, то сначала записываем его в виде дроби как 5/6. Затем умножаем эту дробь на 100:

(5/6) * 100 = 83.33%

Таким образом, соотношение 5:6 можно преобразовать в проценты и составляет около 83.33%.

Соотношение — это способ сравнения двух величин, измеряемых в одних и тех же единицах, чтобы показать, сколько одной величины содержится в другой. Соотношения могут быть разделены на два основных типа: соотношение части к части и соотношение части к целому.

1. Соотношение части к части: Этот тип соотношения используется для описания связи между двумя разными сущностями или группами. Например, если в классе 12 мальчиков и 15 девочек, то соотношение мальчиков к девочкам составляет 12:15. Это означает, что на каждых 12 мальчиков приходится 15 девочек.

2. Соотношение части к целому: Этот тип соотношения используется для определения отношения определенной группы к общему числу. Например, если из 10 человек 5 предпочитают читать книги, то соотношение части (тех, кто любит читать книги) к целому (всего людей) составляет 5:10. Это говорит нам о том, что половина (5 из 10) людей в данной группе увлекаются чтением книг.

Таким образом, соотношения помогают нам понимать, как связаны между собой различные части или группы в контексте общей совокупности.

Формула соотношения используется для сравнения двух чисел или величин. Общая форма представления соотношения между двумя величинами, например, «a» и «b», записывается как «a: b» и читается как «a по отношению к b».

Это соотношение также может быть представлено в виде дроби: «a/b». Для упрощения соотношения используется та же процедура, что и для упрощения обычных дробей: «a:b = a/b». Давайте проиллюстрируем это на примере.

Пример: В классе из 50 учеников 23 девочки, а остальные — мальчики. Нам нужно найти соотношение количества мальчиков к количеству девочек.

1. Общее количество студентов = 50.
2. Количество девочек = 23.
3. Для нахождения количества мальчиков, вычитаем количество девочек из общего числа учеников: Общее количество мальчиков = Общее количество учеников — Количество девочек = 50 — 23 = 27.

Таким образом, соотношение количества мальчиков к количеству девочек равно 27:23.

Для расчета соотношения между двумя величинами, следуйте следующим шагам. Рассмотрим этот процесс на примере приготовления пышных блинов, где требуется 15 стаканов муки и 20 стаканов сахара:

Шаг 1: Определите значения обеих величин, для которых вы хотите найти соотношение. В данном случае это 15 и 20 (мука и сахар).

Шаг 2: Запишите эти значения в виде дроби a/b. Таким образом, мы имеем дробь 15/20.

Шаг 3: Упростите дробь, если это возможно. Упрощенная дробь будет окончательным соотношением. В данном случае 15/20 можно упростить до 3/4.

Шаг 4: Таким образом, соотношение муки к сахару можно выразить как 3:4.

Эти шаги помогают нам найти простое и понятное соотношение между двумя величинами. Вы также можете использовать онлайн-калькулятор коэффициентов для проверки своих ответов при расчете коэффициентов.

Упрощение соотношений делает их более понятными и легкими для анализа. Чтобы упростить соотношение, следуйте этим шагам, как это было описано в вашем тексте:

Шаг 1: Запишите данное соотношение a:b в виде дроби a/b. Ваше исходное соотношение 18:10 можно записать как 18/10.

Шаг 2: Найдите наибольший общий коэффициент (НОК) между числами ‘a’ и ‘b’. В вашем примере НОК между 10 и 18 равен 2.

Шаг 3: Разделите числитель и знаменатель дроби на НОК, чтобы получить упрощенную дробь. В вашем случае, разделив числитель и знаменатель на 2, вы получите (18 ÷ 2) / (10 ÷ 2) = 9/5.

Шаг 4: Представьте эту упрощенную дробь в форме соотношения. Таким образом, упрощенное соотношение будет составлять 9:5.

Советы и рекомендации:

• Перед упрощением удостоверьтесь, что единицы измерения обоих величин совпадают, чтобы соотношение было корректным.
• Если оба числа ‘a’ и ‘b’ в соотношении a:b равны, то соотношение a:b равно 1.
• Если ‘a’ больше чем ‘b’ в соотношении a:b, то a:b будет больше 1.
• Если ‘a’ меньше чем ‘b’ в соотношении a:b, то a:b будет меньше 1.

Эти шаги помогут вам упростить соотношения и легче их интерпретировать. Вы также можете использовать бесплатные онлайн-калькуляторы упрощения коэффициентов для проверки ваших ответов.

Эквивалентные соотношения подобны эквивалентным дробям. Если предшествующий (первый член) и последующий (второй член) в данном соотношении умножаются или делятся на одно и то же число, отличное от нуля, то получается эквивалентное соотношение.

Давайте разберем это на примерах:

1. Исходное соотношение: 1:3. Если умножить оба члена на 3, то получим (1 × 3) : (3 × 3) = 3:9. Здесь 1:3 и 3:9 — это эквивалентные соотношения, так как они выражают одно и то же отношение между двумя величинами.

2. Исходное соотношение: 20:10. Если разделить оба члена на 10, то получим (20 ÷ 10) : (10 ÷ 10) = 2:1. Здесь 20:10 и 2:1 также являются эквивалентными соотношениями.

Вы можете найти бесконечное количество эквивалентных соотношений для любого заданного соотношения, умножая или деля на положительное целое число. Это позволяет представлять одно и то же соотношение в различных формах, что может быть полезным для анализа и сравнения данных.

Таблица коэффициентов представляет собой структурированный список эквивалентных соотношений для заданного исходного соотношения. Эквивалентные соотношения могут быть получены путем умножения или деления обоих членов исходного соотношения на одно и то же число. Давайте рассмотрим пример, чтобы лучше понять, как работает таблица коэффициентов:

Исходное соотношение: 1:4

Таблица эквивалентных соотношений:

1. Умножим оба члена на 2:

   • (1 * 2) : (4 * 2) = 2:8

2. Умножим оба члена на 3:

   • (1 * 3) : (4 * 3) = 3:12

3. Умножим оба члена на 6:

   • (1 * 6) : (4 * 6) = 6:24

4. Умножим оба члена на 9:

   • (1 * 9) : (4 * 9) = 9:36

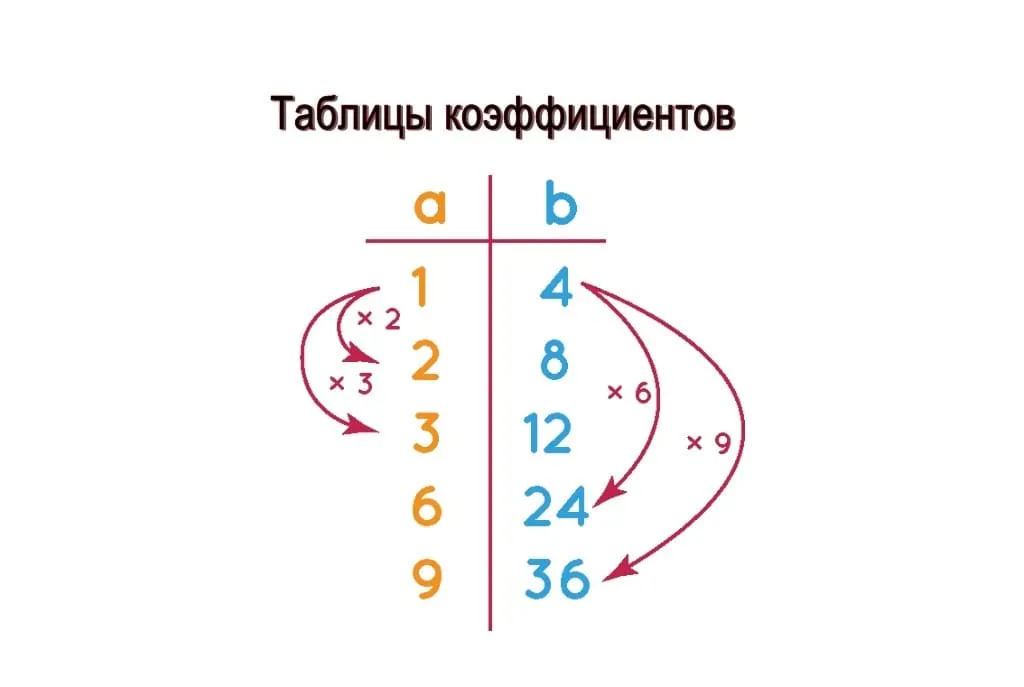
В этой таблице мы видим четыре эквивалентных соотношения, которые связаны умножением числа. Таким образом, 1:4, 2:8, 3:12, 6:24 и 9:36 являются эквивалентными соотношениями, так как они представляют одно и то же отношение между двумя величинами в разных числовых выражениях. Такие таблицы полезны для упрощения и сравнения соотношений в разных формах.

Пример 1:

Задача: В школьном зале 49 мальчиков и 28 девочек. Найдите соотношение числа мальчиков к числу девочек.

Решение:

Исходные данные: количество мальчиков = 49, количество девочек = 28.

1. Найдем наибольший общий коэффициент (НОК) между 49 и 28, который равен 7.

2. Разделим оба члена соотношения на НОК, чтобы упростить его:

   • (49 ÷ 7) : (28 ÷ 7) = 7 : 4.

Ответ: Соотношение числа мальчиков к числу девочек составляет 7:4.

Пример 2:

Задача: В музыкальном классе 30 учеников. 10 из них взрослые, а остальные — дети. Найдите соотношение числа детей к общему числу учащихся в музыкальном классе.

Решение:

Исходные данные: общее количество учащихся = 30, количество взрослых = 10.

1. Найдем количество детей, вычтя количество взрослых из общего числа учащихся:

   • Количество детей = 30 — 10 = 20.

2. Теперь мы можем выразить соотношение числа детей к общему числу учащихся:

   • Соотношение = 20 : 30.

3. Упростим это соотношение, деля оба члена на их НОК, который равен 10:

   • (20 ÷ 10) : (30 ÷ 10) = 2 : 3.

Ответ: Соотношение числа детей к общему числу учащихся в музыкальном классе составляет 2:3.

Пример 3:

Задача: Упростите заданное соотношение 87:75.

Решение:

1. Найдем наибольший общий коэффициент (НОК) между 87 и 75, который равен 3.

2. Разделим оба члена соотношения на НОК, чтобы упростить его:

   • (87 ÷ 3) : (75 ÷ 3) = 29 : 25.

Ответ: Упрощенное соотношение 87:75 равно 29:25.