SAS инструменты Сайт с 1000 ми полезных инструментов и калькуляторов SAS
Умножение и деление степеней
Умный калькулятор степеней и одночленов для школы
Основные формулы (7-11 класс):
Оглавление
Сидите над домашкой по алгебре и путаетесь в показателях? Наш калькулятор степеней — это простой и надёжный инструмент для учеников 7–11 классов, который поможет не только получить ответ, но и понять принцип решения.
В отличие от обычных калькуляторов, этот инструмент «понимает» структуру числа. Если вы введёте умножение 8 · 4, он не просто выдаст 32, а покажет, что это 2³ · 2² = 2⁵. Он умеет работать с одночленами (например, 2x), отрицательными и дробными показателями.
Это идеальный помощник для подготовки к контрольным, ОГЭ и ЕГЭ. Вы увидите каждый шаг: как сокращаются дроби, как складываются или вычитаются степени и как работает правило нулевой степени. Никакой «магии» — только чёткая математическая логика.
Инструкция: как пользоваться калькулятором правильно
Интерфейс спроектирован так, чтобы вы не совершили ошибку при вводе. Внимательно прочитайте назначение полей, так как калькулятор работает по формуле (ka)ⁿ.
Выберите действие:
Вверху переключите режим: «÷ Деление» (для дробей) или «× Умножение».
Заполните поле «Основание / Одночлен»:
Сюда пишем число или буквенное выражение, которое будем возводить в степень.
Важный нюанс: Если вы напишете 2x и укажете степень 3, калькулятор посчитает это как (2x)³, то есть возведёт в куб и двойку, и икс (получится 8x³).
Если у вас просто x⁵, пишите в основание x, а в степень 5.
Заполните поле «Показатель (степень)»:
Здесь указываем саму степень.
Поддерживаются целые числа (2, -5) и дроби (0.5, 1/2).
Получите решение:
Нажмите «⚡ Рассчитать ответ».
Изучите пошаговое объяснение под кнопкой.
Если пример подходит (целые небольшие степени), откроется блок «Визуализация», где точками показано, как сокращаются или объединяются множители.
Примеры использования: разбираем реальные задачи
Посмотрите, как правильно вводить данные, чтобы решать типовые примеры из учебников (например, Виленкина или Мерзляка).
Пример 1: Деление степеней с одинаковыми основаниями
Задача: Упростить выражение (3a)⁵ : (3a)².
Как вводить:
Режим: «÷ Деление».
Первое число: Основание 3a, Показатель 5.
Второе число: Основание 3a, Показатель 2.
Результат: Калькулятор применит правило вычитания показателей: 5 — 2 = 3.
Ответ: (3a)³ или 27a³.
Польза: Вы сразу видите, что при одинаковых основаниях мы работаем только с «верхушками» чисел.
Пример 2: Умножение и поиск общего основания
Задача: Представить произведение 16 · 8 в виде степени с основанием 2.
Как вводить:
Режим: «× Умножение».
Первое число: Основание 16, Показатель 1.
Второе число: Основание 8, Показатель 1.
Результат: Умный алгоритм увидит, что 16 = 2⁴, а 8 = 2³. Он сложит показатели: 4 + 3 = 7.
Ответ: 2⁷ (или 128).
Польза: Незаменимо при решении показательных уравнений в старших классах.
Пример 3: Работа с отрицательной степенью
Задача: Вычислить значение выражения x² : x⁶.
Как вводить:
Режим: «÷ Деление».
Первое число: Основание x, Показатель 2.
Второе число: Основание x, Показатель 6.
Результат: 2 — 6 = -4.
Ответ: x⁻⁴ (или 1/x⁴).
Польза: Наглядно показывает, откуда берётся дробь в ответе и что значит «минус» в степени.
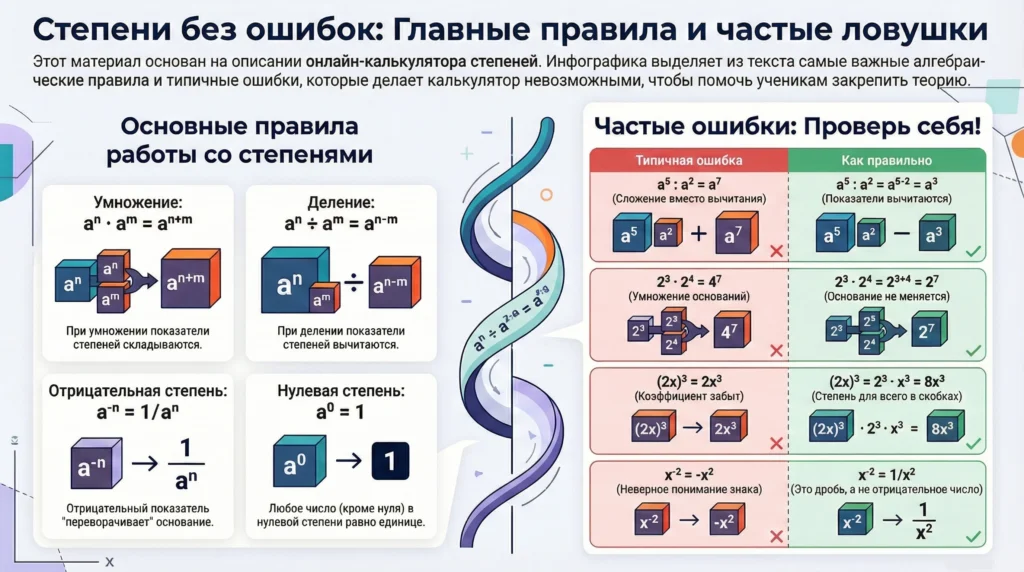
Шпаргалка: где чаще всего ошибаются школьники
Мы собрали популярные ошибки при работе со степенями. Эта таблица поможет вам проверить себя перед сдачей тетради.
| Ошибка ученика | В чём проблема | Правильное решение (как считает калькулятор) |
| Сложение при делении | Путают правила. Пишут a⁵ : a² = a⁷. | При делении показатели вычитаются: a⁵⁻² = a³. |
| Умножение оснований | В примере 2³ · 2⁴ умножают основания: 4⁷. | Основание остаётся прежним, складываются только степени: 2⁷. |
| Минус в степени | Считают, что x⁻² — это отрицательное число (-x²). | Отрицательная степень отправляет число в знаменатель: 1/x². |
| Возведение в степень | При (2x)³ забывают про число и пишут 2x³. | Степень относится ко всему, что в скобках: 2³ · x³ = 8x³. |
| Нулевая степень | Пишут, что 5⁰ = 0. | Любое число в нулевой степени (кроме 0) равно 1. |
Складываются или вычитаются степени при умножении?
При умножении степеней с одинаковыми основаниями их показатели складываются. Само основание остаётся без изменений. Пример: x² · x³ = x⁵.
Как работает деление степеней?
Если основания одинаковые, то из показателя делимого вычитается показатель делителя. Пример: y¹⁰ : y² = y⁸. Если основания разные, сократить их напрямую нельзя (если только это не числа, которые можно привести к общему основанию).
Что значит отрицательная степень?
Отрицательный показатель не делает число отрицательным. Он показывает, что число является обратным. Проще говоря, a⁻ⁿ — это то же самое, что 1 разделённая на aⁿ.
Чему равно число в степени 0?
Запомните простое правило: любое число (кроме самого нуля) в нулевой степени равно единице. Даже если это сложная дробь или огромное выражение в скобках.
Как калькулятор работает с дробями в степени?
Инструмент поддерживает дробные показатели (например, 0.5 или 1/2). Это соответствует извлечению корня. Например, степень 1/2 — это квадратный корень, а 1/3 — кубический.
Можно ли вводить коэффициенты, например 4x?
Да. Учтите, что калькулятор воспринимает запись 4x в поле основания как единое выражение (4x). Если вы поставите степень 2, он возведёт в квадрат и четвёрку (получится 16), и икс.
Поможет ли это при подготовке к ОГЭ/ЕГЭ?
Безусловно. В заданиях экзаменов (особенно №8 в ОГЭ) часто встречаются примеры на свойства степеней. Наш инструмент поможет отработать навык и проверить правильность решения домашних заданий.
Почему aⁿ · bⁿ = (ab)ⁿ?
Это свойство степени произведения. Если у разных оснований одинаковый показатель, их можно объединить под одну скобку. Калькулятор умеет это делать, если включить режим умножения.
