Introduzca la resistencia
Resistencia convertida
1000 Ом
1 kilo ohmio = 1000 ohmios
Tabla de contenido
Este convertidor de resistencia en línea es su asistente confiable en el mundo de la electrónica. Le brinda la capacidad de convertir fácilmente la resistencia de una unidad de medida a otra. Ya sea que estés trabajando con Ohmios, Kilo Ohmios, Mega Ohmios u otras unidades de resistencia, este conversor te permitirá hacerlo rápida y fácilmente.
La interfaz es sencilla e intuitiva. Solo necesita ingresar el valor de resistencia y seleccionar la unidad de medida actual. Luego seleccione la unidad de medida deseada a la que desea convertir la resistencia. Una vez que hagas esto, el convertidor te dará instantáneamente el resultado. Inmediatamente verás cuánto será en la nueva unidad de medida.
Por ejemplo, si necesita saber cuánto es 1 kilo ohmio en ohmios, este conversor lo hará por usted y obtendrá la respuesta: 1000 ohmios. ¡Es tan simple!
Además, el conversor también te proporciona la fórmula de conversión, para que siempre puedas entender cómo se realiza el cálculo. Esta es una gran herramienta para estudiantes, ingenieros y cualquier persona que trabaje con electrónica y resistencia.
Ahorre tiempo y simplifique sus cálculos con este cómodo e intuitivo convertidor de resistencia.
Концепция сопротивления: Простое объяснение каждой единицы измерения
Ом (Ω): Ом — это основная единица измерения сопротивления. Она обозначается символом «Ω» и используется для измерения электрического сопротивления в цепи. 1 Ом равен сопротивлению, при котором приложение напряжения в 1 вольт к цепи создает ток в 1 ампер.
Абом (abΩ): Абом — это очень маленькая единица измерения сопротивления, которая обозначается символом «abΩ». Она используется в микроэлектронике и нанотехнологиях для измерения сопротивления в миллиардных долях Ома.
Гига Ом (GΩ): Гига Ом — это единица измерения, которая обозначается символом «GΩ». Она используется для измерения очень высоких значений сопротивления, равных миллиардам Омов.
Мега Ом (MΩ): Мега Ом — это единица измерения, которая обозначается символом «MΩ». Она используется для измерения значительных значений сопротивления, равных миллионам Омов.
Кило Ом (kΩ): Кило Ом — это единица измерения, которая обозначается символом «kΩ». Она применяется для измерения сопротивления, равного тысячам Омов.
Микро Ом (µΩ): Микро Ом — это маленькая единица измерения, обозначаемая символом «µΩ». Она используется для измерения сопротивления, которое очень мало и составляет миллионных долей Ома.
Милли Ом (mΩ): Милли Ом — это единица измерения, которая обозначается символом «mΩ». Она используется для измерения небольших значений сопротивления, равных тысячным долям Ома.
Нано Ом (nΩ): Нано Ом — это очень маленькая единица измерения, обозначаемая символом «nΩ». Она применяется для измерения сопротивления, которое крайне мало и составляет миллиардных долей Ома.
Эти различные единицы измерения сопротивления используются в зависимости от масштаба и точности измерения, что позволяет инженерам и ученым работать с разнообразными значениями сопротивления в различных областях науки и техники.
Сопротивление в электричестве: Ключевой параметр для контроля потока тока
Сопротивление в электричестве представляет собой меру того, насколько материал или устройство затрудняют прохождение электрического тока через себя. Это важное понятие в области электрических цепей и электроники. Сопротивление измеряется в Омах (Ω) и обозначается символом «Ω».
Почему сопротивление так важно:
Контроль тока: Сопротивление является фундаментальным параметром для контроля электрического тока в цепи. Оно определяет, как сильно ток будет «затормаживаться» при прохождении через элемент. Это позволяет управлять интенсивностью тока в цепи, что важно для безопасности и правильной работы устройств.
Потери энергии: Сопротивление также играет роль в потерях энергии в электрических цепях. Когда ток проходит через материал сопротивления, часть энергии преобразуется в тепло. Это важно учитывать при проектировании электрических систем, чтобы минимизировать потери и повысить эффективность.
Деление напряжения: Сопротивление используется для деления напряжения в цепи. Это позволяет создавать различные уровни напряжения для различных компонентов в электронических устройствах.
Фильтрация сигналов: В электронике сопротивления могут использоваться для фильтрации сигналов. Например, фильтры с низким сопротивлением пропускают большой диапазон частот, тогда как фильтры с высоким сопротивлением ограничивают частотный диапазон.
Датчики и измерения: Множество датчиков, таких как термисторы и фоторезисторы, используют сопротивление для измерения физических параметров, например, температуры или освещенности.
Сопротивление играет критическую роль в электронике, электрических схемах и электрических устройствах. Понимание и управление этим параметром позволяют инженерам и электронщикам создавать эффективные и безопасные электрические системы, что является ключевым элементом в современной технике и технологиях.
Закон Ома
Закон Ома представляет собой фундаментальный принцип в электрических цепях, который объясняет взаимосвязь между напряжением, током и сопротивлением. Этот закон гласит, что сила тока (I), протекающего через проводник между двумя точками, прямо пропорциональна напряжению (V), приложенному к этому проводнику, и обратно пропорциональна его сопротивлению (R). Вот формулы, которые описывают этот закон:
Напряжение (V) равно произведению силы тока (I) на сопротивление (R): V = I × R
Сопротивление (R) равно напряжению (V), деленному на силу тока (I): R = V / I
Сила тока (I) равна напряжению (V), деленному на сопротивление (R): I = V / R
Этот закон применим к многим материалам и компонентам в широком диапазоне напряжений и токов. Он остается верным даже в случае изменения напряжения (переменного тока) или при использовании постоянного тока. Это фундаментальное правило помогает инженерам и ученым в понимании и управлении электрическими цепями и устройствами.
Электрическая мощность
Мощность в электрических системах представляет собой скорость передачи электрической энергии через цепь в единицу времени. Обычно она измеряется в ваттах в системе Международных единиц (СИ). Эта энергия обычно производится генераторами и поставляется на предприятия и в дома через системы электроснабжения. Она также может быть снабжена из электрических батарей и других источников.
В случае резистивных цепей закон Джоуля и закон Ома могут быть объединены для определения мощности, рассеиваемой в цепи. Вот несколько формул, которые описывают мощность:
Мощность (P) равна произведению напряжения (V) на силу тока (I): P = V × I
Мощность (P) также может быть выражена как квадрат напряжения (V) деленный на сопротивление (R): P = V^2 / R
Или как произведение квадрата силы тока (I) на сопротивление (R): P = I^2 × R
Эти формулы помогают расчитать количество мощности, которое тратится или вырабатывается в электрических цепях, и являются важными величинами для электротехнических расчетов и проектирования систем электроснабжения.
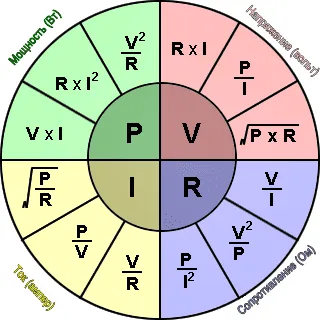
Колесо формулы закона Ома
Ниже приведено колесо формул для отношений Закона Ома между P, I, V и R. По сути, это то, что делает калькулятор, и это просто представление алгебраических манипуляций с уравнениями выше. Чтобы использовать колесо, выберите переменную для решения в середине колеса, затем используйте соотношение для двух известных переменных в поперечном сечении круга.
Единицы измерения удельного сопротивления и проводимости
Удельное сопротивление (ρ) и проводимость (σ) — это важные свойства материалов, которые определяют их способность проводить электрический ток. Давайте разберемся в единицах измерения этих величин:
Удельное сопротивление (ρ) — это мера того, насколько материал затрудняет прохождение электрического тока. Удельное сопротивление зависит от самого материала и не зависит от геометрии проводника. Единицей измерения удельного сопротивления в Международной системе единиц (СИ) является ом-метр (Ом·м).
Проводимость (σ) — это обратная величина удельного сопротивления и описывает способность материала проводить электрический ток. Проводимость также является внутренним свойством материала. Единицей измерения проводимости в СИ является сименс на метр (См/м).
Для удобства, проводимость (σ) обратно пропорциональна удельному сопротивлению (ρ), и они связаны уравнением:
σ = 1 / ρ
Это означает, что если материал имеет высокое удельное сопротивление, то его проводимость будет низкой, и наоборот.
Сверхпроводимость — это интересное явление, при котором удельное сопротивление материала падает до нуля при очень низких температурах, и проводимость становится практически бесконечной. Это позволяет электрическому току проходить через материал без потерь, и такие материалы называются сверхпроводниками. Это связано с фундаментальными квантовыми эффектами и имеет важные приложения в современной науке и технологии, включая магнитные левитационные системы.
Формула проводимости и формула сопротивления
Для более глубокого понимания проводимости и сопротивления в проводниках, давайте рассмотрим соответствующие формулы более подробно:
Формула сопротивления (R): Сопротивление (R) проводника зависит от его удельного сопротивления (ρ), длины (L) и площади поперечного сечения (A). Формула сопротивления выглядит следующим образом: R = ρ * L / A
- R — сопротивление в омах (Ом).
- ρ — удельное сопротивление материала в ом-метрах (Ом·м).
- L — длина провода в метрах (м).
- A — площадь поперечного сечения провода в квадратных метрах (м^2).
Эта формула позволяет рассчитать сопротивление проводника, учитывая его физические параметры и материал.
Формула проводимости (G): Проводимость (G) проводника зависит от его проводимости (σ), площади поперечного сечения (A) и длины (L), и она обратно пропорциональна сопротивлению. Формула проводимости выглядит следующим образом: G = σ * A / L
- G — проводимость в сименсах (См).
- σ — проводимость материала в сименсах на метр (См/м).
- A — площадь поперечного сечения провода в квадратных метрах (м^2).
- L — длина провода в метрах (м).
Эта формула позволяет рассчитать проводимость проводника, учитывая его физические параметры и проводимость материала.
Обе формулы имеют важное значение при проектировании и анализе электрических цепей, так как позволяют определить, как проводники взаимодействуют с электрическим током в зависимости от их материала и геометрии.
Проводимость меди и удельное сопротивление меди
Медь является отличным проводником электричества благодаря ее низкому удельному сопротивлению и высокой проводимости. Давайте рассмотрим её характеристики подробнее:
Удельное сопротивление меди (ρ): Удельное сопротивление меди при комнатной температуре (20°C) составляет приближенно 1,68 × 10^(-8) Ом·м. Это очень низкое значение, что означает, что медь практически не затрудняет прохождение электрического тока.
Проводимость меди (σ): Проводимость меди при 20°C приближенно равна 5,95 × 10^7 См/м. Это высокое значение проводимости делает медь одним из наилучших материалов для проводников, так как она способствует свободному движению электронов под действием электрического поля.
Эти характеристики делают медь идеальным материалом для производства электрических проводов и кабелей. Медные провода широко используются в электротехнике и электронике, так как они обеспечивают надежную передачу электрического тока с минимальными потерями из-за сопротивления проводника.
Удельное сопротивление и проводимость материала могут изменяться с изменением температуры. Поэтому при работе с электрическими системами важно учитывать эти изменения и проводить необходимые расчеты и коррекции, особенно если эксплуатация происходит в экстремных условиях температуры.
Как рассчитать сопротивление провода?
Для расчета сопротивления провода используйте следующую формулу:
R = ρ * L / A
Donde:
- R — сопротивление провода в омах (Ω).
- ρ — удельное сопротивление материала провода в омах на метр (Ω·м). Удельное сопротивление зависит от материала провода и может изменяться с температурой.
- L — длина провода в метрах (м).
- A — площадь поперечного сечения провода в квадратных метрах (м²).
Шаги для расчета сопротивления провода:
Определите материал провода и найдите значение его удельного сопротивления (ρ) при данной температуре. Обычно это значение указывается в литературе или предоставляется производителем материала.
Измерьте длину провода (L), для которой вы хотите рассчитать сопротивление.
Определите площадь поперечного сечения провода (A). Площадь поперечного сечения зависит от формы провода. Для круглого провода площадь можно рассчитать по формуле: A = π * r², где r — радиус провода.
Используйте формулу R = ρ * L / A для расчета сопротивления провода.
Пример расчета: Допустим, у вас есть медный провод длиной 10 метров с круглым сечением радиусом 0,001 метра (1 миллиметр). Удельное сопротивление меди при комнатной температуре составляет приближенно 1,68 × 10^(-8) ом·м.
- ρ (удельное сопротивление меди) = 1,68 × 10^(-8) ом·м
- L (длина провода) = 10 метров
- A (площадь поперечного сечения провода) = π * (0,001 метра)² = 3,1415 × 10^(-6) м²
Теперь, подставив эти значения в формулу, вы можете рассчитать сопротивление провода:
R = (1,68 × 10^(-8) ом·м) * (10 м) / (3,1415 × 10^(-6) м²) ≈ 0,0532 ома
Таким образом, сопротивление этого 10-метрового медного провода с площадью поперечного сечения 1 миллиметр в квадрате составляет приближенно 0,0532 ома при комнатной температуре.
Как длина провода влияет на сопротивление?
Длина провода имеет прямое влияние на его сопротивление. Сопротивление провода пропорционально его длине. Это означает, что при увеличении длины провода, сопротивление также увеличивается, и наоборот, при уменьшении длины, сопротивление уменьшается.
Это связано с тем, что каждый проводник имеет определенное удельное сопротивление (ρ), которое характеризует его способность проводить электрический ток. Удельное сопротивление зависит от материала провода и может изменяться в зависимости от температуры. Однако длина провода (L) также является важным фактором в формуле для расчета сопротивления (R):
R = ρ * L / A
Donde:
- R — сопротивление провода.
- ρ — удельное сопротивление материала провода.
- L — длина провода.
- A — площадь поперечного сечения провода.
Как видно из этой формулы, чем длиннее провод, тем больше сопротивление. Это объясняется тем, что при увеличении длины провода увеличивается «путь» для электронов, которые несут электрический ток, и этот путь представляет собой дополнительное сопротивление для тока.
Поэтому при проектировании электрических систем и расчетах сопротивления проводов важно учитывать их длину, особенно если проводы имеют большую протяженность или если требуется минимизировать потери энергии из-за сопротивления.
Как площадь провода влияет на сопротивление?
Площадь поперечного сечения провода также имеет значительное влияние на его сопротивление. Сопротивление провода обратно пропорционально площади поперечного сечения: чем больше площадь, тем меньше сопротивление, и наоборот.
Это основано на формуле для расчета сопротивления провода:
R = ρ * L / A
Donde:
- R — сопротивление провода.
- ρ — удельное сопротивление материала провода.
- L — длина провода.
- A — площадь поперечного сечения провода.
Когда площадь поперечного сечения провода увеличивается, знаменатель в формуле становится больше, что ведет к уменьшению сопротивления. Это происходит потому, что увеличение площади создает больше путей для электронов, несущих электрический ток, чтобы свободно двигаться внутри провода.
Следовательно, провода с большой площадью поперечного сечения имеют меньшее сопротивление и могут более эффективно передавать электрический ток без значительных потерь энергии из-за сопротивления. Это особенно важно в электротехнике и электронике, где нужно минимизировать потери энергии в электрических цепях.
Какие четыре фактора влияют на сопротивление провода?
Четыре основных фактора, которые влияют на сопротивление провода:
Длина провода (L): Длина провода прямо пропорционально влияет на его сопротивление. Чем длиннее провод, тем больше сопротивление, так как ток должен пройти более длинное расстояние, что создает дополнительное сопротивление.
Площадь поперечного сечения провода (A): Площадь поперечного сечения обратно пропорционально влияет на сопротивление. Чем больше площадь сечения, тем меньше сопротивление, так как большая площадь позволяет более свободному движению электронов, несущих ток.
Материал провода: Удельное сопротивление (и проводимость) материала провода сильно влияют на сопротивление. Разные материалы имеют различные удельные сопротивления, и некоторые материалы лучше проводят электрический ток, чем другие. Медь, например, имеет низкое удельное сопротивление и является одним из лучших проводников.
Температура материала: Температура также влияет на удельное сопротивление материала провода. Обычно с увеличением температуры удельное сопротивление материала увеличивается. Это важно учитывать при работе с проводами, особенно в высокотемпературных условиях.
Исходя из этих четырех факторов, можно провести расчеты и выбрать соответствующий провод для конкретных электрических задач с учетом необходимой длины, площади сечения, материала и условий эксплуатации.
 Sitio web con 1000 mi útiles herramientas y calculadoras SAS Recursos en línea gratuitos con más de 1000 herramientas y calculadoras SAS. Nuestro sitio ofrece una variedad de servicios que incluyen un constructor de ventanas emergentes, un constructor de widgets, un constructor de tarjetas de visita, un generador de códigos QR, un acortador de enlaces con análisis, así como herramientas de descarga de vídeos y de correspondencia de nombres de dominio.
Sitio web con 1000 mi útiles herramientas y calculadoras SAS Recursos en línea gratuitos con más de 1000 herramientas y calculadoras SAS. Nuestro sitio ofrece una variedad de servicios que incluyen un constructor de ventanas emergentes, un constructor de widgets, un constructor de tarjetas de visita, un generador de códigos QR, un acortador de enlaces con análisis, así como herramientas de descarga de vídeos y de correspondencia de nombres de dominio. 
