Debe ingresar: Ingrese las coordenadas de la ubicación A, Ingrese las coordenadas de la ubicación B, Haga clic en la flecha amarilla >> para calcular .
(La ubicación predeterminada es la sede de Google).
De forma predeterminada, se establece la ubicación de la sede de Yandex.
Tabla de contenido
Представляем вашему вниманию удивительно удобный и точный онлайн калькулятор для определения расстояния между двумя точками на карте, а также разницы во времени между восходом солнца. Этот инструмент станет незаменимым помощником как для путешественников, так и для профессионалов, занимающихся логистикой или геодезией.
Основное преимущество нашего калькулятора – его простота и интуитивно понятный интерфейс. Вам не нужно быть экспертом в области картографии или владеть специальными знаниями, чтобы легко рассчитать интересующее вас расстояние. Всё, что от вас требуется – это ввести координаты начальной и конечной точек вашего маршрута.
Благодаря продвинутым алгоритмам расчёта, калькулятор обеспечивает высокую точность измерений. Вы можете быть уверены в том, что полученные данные о расстоянии будут максимально приближены к реальности. Это делает инструмент идеальным выбором для планирования путешествий, маршрутов доставки или любых других задач, где важна точность расчётов.
Использование калькулятора не ограничивается лишь определением расстояний. Он также позволяет вычислить разницу во времени между восходом солнца в различных точках, что особенно полезно для любителей астрономии или фотографов, желающих запечатлеть уникальные моменты природы.
Наш калькулятор доступен для использования абсолютно бесплатно. Мы стремимся сделать полезные инструменты доступными для широкого круга пользователей. Просто перейдите по ссылке, и вы сразу же сможете воспользоваться всеми функциями калькулятора без каких-либо ограничений.
Заключительно, хотелось бы подчеркнуть, что при разработке калькулятора особое внимание уделялось удобству и простоте использования. Все элементы интерфейса оптимизированы таким образом, чтобы пользователь мог легко найти необходимую функцию и получить результаты расчётов в кратчайшие сроки.
Опробуйте наш калькулятор уже сегодня, и убедитесь в его неоспоримых преимуществах самостоятельно!
Инструкция по заполнению формы калькулятора расстояния
Этот калькулятор создан для удобного определения расстояния между двумя точками на Земле, а также для расчета разницы во времени восхода солнца между этими точками. Вот подробное руководство о том, как правильно заполнить форму для получения наиболее точных результатов.
Шаг 1: Ввод координат первой точки
Поле для широты (Latitude): Введите широту первой точки. Широта измеряется в градусах и может быть северной (N) или южной (S). Пример: если ваша точка находится в Северном полушарии, введите значение широты как положительное число, например, 37.3894 для штаб-квартиры Google.
Выбор полушария для широты: Выберите N (северное) или S (южное) из выпадающего списка, в зависимости от того, в каком полушарии находится ваша точка.
Поле для долготы (Longitude): Введите долготу первой точки. Долгота также измеряется в градусах и может быть западной (W) или восточной (E). Пример: 122.0819 для штаб-квартиры Google, обозначается как западная долгота.
Выбор полушария для долготы: Выберите W (западное) или E (восточное) из выпадающего списка для долготы.
Шаг 2: Ввод координат второй точки
Повторите шаги 1-4 для второй точки, используя поля для ввода широты и долготы второго местоположения. Пример: для штаб-квартиры Яндекс введите широту 55.733842 и долготу 37.588144, выбрав соответствующие полушария.
Важные моменты при заполнении
Точность координат: Чем точнее вы введете координаты, тем более точным будет расчет расстояния. Используйте десятичные градусы для большей точности.
Полушария: Правильный выбор полушария критически важен для точности расчетов. Убедитесь, что вы правильно указали, находится ли точка в северном или южном, западном или восточном полушарии.
Использование точек и запятых: В качестве десятичного разделителя используйте точку.
После заполнения формы
После того как все поля заполнены, нажмите на кнопку с двойной стрелкой для расчета. Калькулятор обработает введенные данные и выведет расстояние между точками в километрах, а также разницу во времени восхода солнца.
Используя эту инструкцию, вы легко сможете пользоваться калькулятором для планирования путешествий, исследования географических объектов или любых других целей, требующих точного знания расстояний и временных различий.
Примеры демонстрирующие использования калькулятора расстояния
Давайте рассмотрим несколько примеров использования онлайн калькулятора для решения различных задач:
Планирование путешествия
Tarea: Вы хотите спланировать автомобильное путешествие из Москвы в Санкт-Петербург и хотите узнать расстояние между этими городами.
Pasos de la solución:
- Введите координаты Москвы (широта: 55.7558, долгота: 37.6173) и Санкт-Петербурга (широта: 59.9343, долгота: 30.3351) в соответствующие поля калькулятора.
- Выберите полушария (N и E) для обеих точек.
- Нажмите на кнопку для расчета.
Resultados del cálculo: Расстояние между Москвой и Санкт-Петербургом составляет примерно 634 километра.
Aplicación en la práctica: Зная расстояние, вы можете спланировать остановки для отдыха и заправки, рассчитать примерное время в пути и стоимость топлива.
Логистика доставки
Tarea: Компания по доставке товаров хочет определить расстояние между своим складом в Новосибирске и пунктом выдачи в Иркутске для расчета стоимости доставки.
Pasos de la solución:
- Введите координаты Новосибирска (широта: 55.0084, долгота: 82.9357) и Иркутска (широта: 52.2864, долгота: 104.2807) в калькулятор.
- Установите N и E для обеих точек.
- Произведите расчет.
Resultados del cálculo: Расстояние между Новосибирском и Иркутском около 1086 километров.
Aplicación en la práctica: Используя эти данные, компания может рассчитать стоимость перевозки груза, оптимизировать маршруты доставки и предложить клиентам наиболее выгодные условия.
Организация мероприятий
Tarea: Организатор мероприятий хочет выбрать наиболее удобное место для участников, приехавших из разных городов, и рассчитать среднее расстояние до места проведения.
Pasos de la solución:
- Используйте калькулятор для определения расстояния от каждого города до места проведения мероприятия.
- Введите координаты городов участников и места проведения мероприятия поочередно.
- Выполните расчет для каждой пары координат.
Resultados del cálculo: Допустим, расстояния от трех городов до места проведения составили 200, 300 и 400 км соответственно.
Aplicación en la práctica: Среднее расстояние до места проведения мероприятия поможет организаторам выбрать наиболее центральное и удобное для всех участников место.
Исследовательский проект
Tarea: Ученые хотят измерить расстояние между двумя точками на местности для экологического исследования.
Pasos de la solución:
- Введите точные координаты исследуемых точек в калькулятор.
- Убедитесь, что выбраны правильные полушария.
- Нажмите для выполнения расчета.
Resultados del cálculo: Допустим, расстояние между точками составило 15 километров.
Aplicación en la práctica: Эти данные помогут ученым определить границы исследуемой территории, рассчитать площадь участка или спланировать маршрут исследовательской экспедиции.
Эти примеры показывают, как калькулятор расстояний может быть использован в различных сферах деятельности, предоставляя точные и полезные данные для планирования и принятия обоснованных решений.
Таблица координаты популярных туристических достопримечательностей мира
Таблица служит справочником для определения координат интересных мест по всему миру. Эта таблица поможет вам быстро находить координаты для расчётов и планировать маршруты или учебные задания.
| Название места | Широта (N) | Долгота (E/W) | Краткое описание |
|---|---|---|---|
| Эйфелева башня, Париж, Франция | 48.8584 | 2.2945 E | Знаменитая железная башня в центре Парижа, символ Франции. |
| Статуя Свободы, Нью-Йорк, США | 40.6892 | 74.0445 W | Одна из самых известных статуй в мире, символ свободы и демократии. |
| Колизей, Рим, Италия | 41.8902 | 12.4922 E | Древний римский амфитеатр, одно из новых семи чудес света. |
| Тадж-Махал, Агра, Индия | 27.1751 | 78.0421 E | Величественный мавзолей, построенный императором Шахджаханом в память о его жене. |
| Великая Китайская стена, Китай | 40.4319 | 116.5704 E | Серия укреплений, протянувшихся на тысячи километров, одно из величайших строительных чудес. |
| Мачу-Пикчу, Перу | 13.1631 | 72.5450 W | Древний город инков, расположенный на вершине горы в Андах. |
| Пирамиды Гизы, Египет | 29.9792 | 31.1342 E | Самые древние и единственные сохранившиеся из семи чудес древнего мира. |
| Сиднейский оперный театр, Австралия | 33.8568 | 151.2153 E | Один из самых знаменитых и узнаваемых зданий XX века, иконическое здание в Сиднее. |
Эта таблица будет полезна для туристов, студентов, исследователей и любителей географии для планирования путешествий, учебных проектов или просто для удовлетворения любопытства о различных местах мира. Используя координаты из таблицы в калькуляторе, можно легко рассчитать расстояние между любыми двумя точками, указанными в таблице, или определить расстояние от своего текущего местоположения до интересующей достопримечательности. Это также может служить отличным инструментом для образовательных учреждений, облегчая планирование экскурсий и учебных поездок.
| № | Интересное место | Регион/Город | Широта | Долгота | Descripción |
|---|---|---|---|---|---|
| 1 | Кремль | Москва | 55.752023 | 37.617499 | Историческая крепость в центре Москвы, включает в себя дворцы и соборы |
| 2 | Эрмитаж | Санкт-Петербург | 59.939095 | 30.315868 | Один из крупнейших художественных и культурно-исторических музеев мира |
| 3 | Эльбрус | Кабардино-Балкария | 43.349953 | 42.445186 | Самая высокая точка России и Европы, популярное место для альпинизма |
| 4 | Валдайский национальный парк | Новгородская область | 57.974724 | 33.252478 | Национальный парк, известный своими озерами и лесами |
| 5 | Каменные столбы Ленские | Республика Саха | 60.556944 | 117.471389 | Уникальный природный парк с каменными столбами высотой до 100 метров |
| 6 | Замок Святого Игнатия | Крым, Бахчисарай | 44.751388 | 33.875000 | Исторический замок на скале, предлагает захватывающие виды на окрестности |
| 7 | Мыс Фиолент | Крым, Севастополь | 44.499444 | 33.491667 | Живописный мыс на Черном море с кристально чистой водой и утесами |
| 8 | Царское Село | Санкт-Петербург | 59.717000 | 30.395000 | Знаменитый архитектурно-парковый ансамбль, включающий Екатерининский дворец |
| 9 | Рускеала | Карелия | 61.775833 | 30.556944 | Горный парк с уникальным мраморным каньоном |
| 10 | Долина Гейзеров | Камчатка | 54.429167 | 160.138333 | Единственное в своем роде место в России, где можно увидеть действующие гейзеры |
| 11 | Кижи | Карелия | 62.073333 | 35.223333 | Остров на Онежском озере с историческим архитектурным комплексом, включающим деревянные церкви |
| 12 | Петропавловская крепость | Санкт-Петербург | 59.950000 | 30.316667 | Основанная Петром Великим, крепость сыграла ключевую роль в истории города |
Эта таблица может быть использована для планирования путешествий по России, помогая выбрать направления и оценить расстояния между различными достопримечательностями. Используйте координаты из таблицы для расчета расстояний с помощью калькулятора, чтобы оптимизировать ваш маршрут и сделать ваше путешествие максимально насыщенным и интересным.
Что такое расстояние?
Расстояние — это мера между двумя точками. Перед тем как мы перейдем к вычислению расстояний, давайте уточним, что это такое. Самое распространенное представление о расстоянии — это пространство между двумя точками. Это определение выражает то, как мы обычно воспринимаем расстояние, но оно не единственное.
В следующих разделах мы узнаем, что понятие расстояния можно расширить за пределы простой длины. Это важно для теории относительности Альберта Эйнштейна.
Если мы говорим о геометрическом определении расстояния, нам нужно выбрать, в каком пространстве мы работаем. Обычно мы имеем дело с трех измерениями или меньше, потому что это более легко воспринимать. В данном калькуляторе мы рассматриваем только двумерное расстояние (включая одномерное как частный случай).
Для определения расстояния между двумя точками, нам нужны сами точки и их координаты в пространстве. В двумерном пространстве каждая точка описывается двумя уникальными координатами. Если вам нужно найти расстояние между точками в одномерном пространстве, вы можете использовать этот калькулятор, установив одинаковые координаты для обеих точек. Однако давайте сосредоточимся на двумерном расстоянии.
Если мы хотим быть математически точными, нам нужно определить тип пространства, в котором мы работаем. Обычно это евклидово пространство, так как оно является «по умолчанию» и используется в большинстве геометрических расчетов.
Формула расстояния для евклидова расстояния
Евклидово пространство, которое мы часто представляем как обычное 2D-пространство, до того, как мы погружаемся в математические дебри, отличается от других пространств. В нем сумма углов в треугольнике всегда равна 180 градусам, и углы в квадратах всегда равны 90 градусам — это нам знакомо из школьной геометрии. Евклидово пространство может быть многомерным, но остается верным его основным правилам, если только у нас есть конечное количество измерений.
Давайте рассмотрим некоторые другие типы пространств. Одним из них является пространство Минковского, которое играет важную роль в физике, особенно в теории относительности и теории поля. Оно похоже на евклидово пространство, но имеет внутреннее скалярное произведение, которое добавляет интересные математические свойства.
Важно понимать, что и евклидово пространство, и пространство Минковского являются плоскими пространствами, где кратчайшее расстояние между двумя точками всегда прямая линия. Однако есть искривленные пространства, где кратчайшее расстояние не всегда является прямой линией. Например, представьте себе пространство, изогнутое в форме сферы. В таком пространстве даже кратчайшее расстояние между точками не будет прямой линией из-за искривления.
Интересным моментом является то, что некоторые линии в таких искривленных пространствах могут пересекаться, что создает удивительные эффекты. Например, линии долготы на Земле, которые пересекаются на полюсах, служат примером этой искривленности.
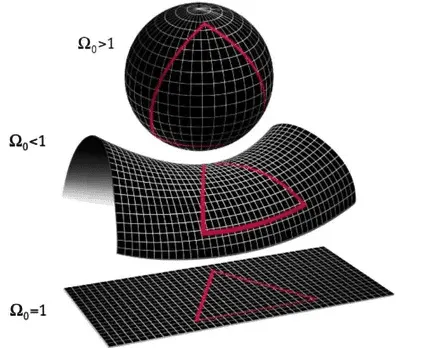
Важно отметить, что концептуально это ОЧЕНЬ отличается от изменения координат. Когда мы возьмем стандартные координаты x, y, z и переведем их в полярные, цилиндрические или даже сферические координаты, мы все равно будем в евклидовом пространстве. Когда мы говорим об искривленном пространстве, мы говорим о совершенно другом пространстве с точки зрения его внутренних свойств. В сферических координатах у вас все еще может быть прямая линия, и расстояние по-прежнему измеряется по прямой линии, даже если это будет очень сложно выразить в цифрах.
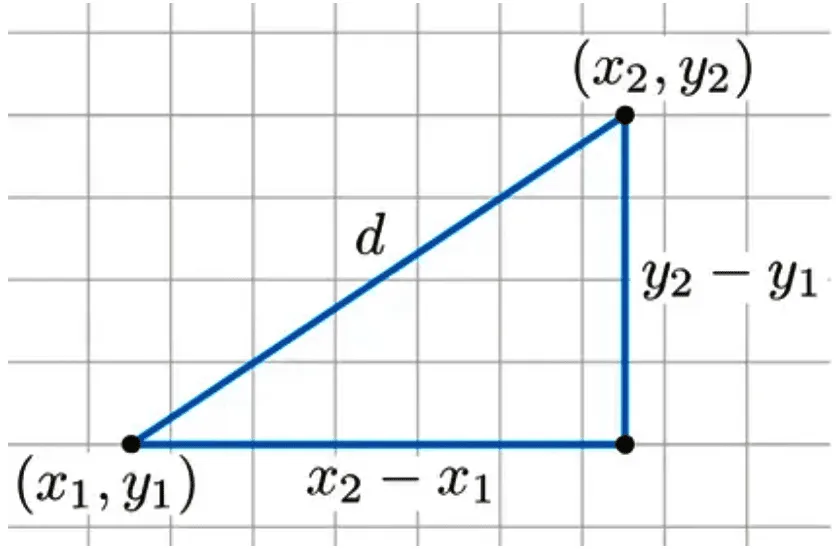
Возвращаясь к евклидову пространству, теперь мы можем представить вам формулу расстояния, которую мы обещали в начале. Формула расстояния
√[(x₂ - x₁)² + (y₂ - y₁)²]
Что относится к теореме Пифагора: a² + b² = c². Здесь a и b — катеты прямоугольного треугольника, а c — гипотенуза. Предположим, что две точки (x₁, y₁) и (x₂, y₂) являются координатами концов гипотенузы. Тогда (x₂ – x₁)² в уравнении расстояния соответствует a² и (y₂ – y₁)² соответствует b². Поскольку c = √(a² + b²), вы можете понять, почему это всего лишь расширение теоремы Пифагора.
Расширенное применение расстояния между точками можно найти в постулате сложения сегментов, который включает в себя нахождение длины сегмента, когда 3 точки лежат на одной прямой.
Расстояние до любой непрерывной структуры
Формула расстояния, о которой мы говорили, это обычная евклидова формула для измерения расстояния между двумя точками. Однако в реальных задачах нам часто нужно вычислить расстояние не только между двумя точками, а, скажем, от точки до линии или окружности. Для этого нам сначала нужно определить, какую конкретную точку на этой линии или окружности мы будем использовать для вычисления расстояния. Затем мы можем применить ту же формулу, которую мы видели ранее.
Здесь важной концепцией является перпендикулярная линия. Расстояние между точкой и непрерывным объектом определяется через перпендикуляр. Геометрический способ измерения расстояния между двумя точками заключается в создании прямой линии между ними и измерении длины этой линии. Однако, когда речь идет о измерении расстояния от точки до линии, возникает вопрос: «Какую линию выбрать из всех возможных?». В этом случае правильный ответ: линия, которая перпендикулярна к исходной линии. Если точка лежит на самой линии, расстояние будет равно нулю. В одномерных случаях мы можем просто рассматривать расстояние между точками, так как линия представляет всего одно измерение.
Это ограничивает некоторые интересные геометрические задачи. Например, мы могли бы определить высоту треугольника как расстояние от одной вершины до противоположной стороны треугольника. В этом случае и площадь треугольника будет зависеть от расстояния, так как площадь является функцией высоты треугольника.
Расстояние до линии и между двумя линиями
Рассмотрим, как измерить расстояние от точки до прямой линии и между двумя линиями в двумерном пространстве. Для вычисления расстояния от точки до прямой линии, есть два способа. Первый способ — следовать шаг за шагом и вычислить отрезок, идущий перпендикулярно к линии от линии до точки, а затем найти его длину. Однако существует более удобное уравнение для этого: d = |Ax1 + By1 + C| / √(A^2 + B^2), где линия задана уравнением Ax + By + C = 0, а точка определена координатами (x1, y1).
Однако обычно линию задают уравнением вида y = mx + b, поэтому нам нужно преобразовать его в форму, удобную для использования в предыдущем уравнении: y = mx + b → mx — y + b = 0. Таким образом, A = m, B = -1 и C = b. Подставив это в предыдущее уравнение, мы получаем: d = |mx1 — y1 + b| / √(m^2 + 1).
Чтобы вычислить расстояние между двумя линиями, достаточно найти длину отрезка, проведенного перпендикулярно к обеим линиям. Для этого можно использовать формулу: d = |C2 — C1| / √(A^2 + B^2), где линии задаются уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0. Если линии параллельны, то A1 = A2 = A и B1 = B2 = B, и формулу можно упростить. Например, для линий y = m1x + b1 и y = m2x + b2, расстояние можно вычислить как d = |b2 — b1| / √(m^2 + 1), где m1 = m2 = m.
Важно отметить, что для параллельных линий расстояние между ними равно нулю, так как они соприкасаются в какой-то точке. Также стоит упомянуть о концепции средней точки, которая находится ровно посередине между двумя другими точками и определяется как точка, находящаяся на одинаковом расстоянии от каждой из опорных точек. Эту концепцию можно обобщить для других фигур, например, центр круга или сферы всегда является средней точкой этой фигуры.
Расстояние между городами
Давайте поговорим о том, как можно узнать расстояние между городами и как это может быть полезно для планирования поездок. Этот процесс можно сравнить с использованием газового калькулятора при планировании вашего путешествия. Представьте, что вы собираетесь путешествовать из города A в город B, и единственная запланированная остановка у вас будет в городе C. Важно отметить, что маршрут от A до B будет пересекать маршрут от B до C под прямым углом. Таким образом, мы сможем определить расстояние между городами A и B. Затем, с помощью газового калькулятора, вы сможете рассчитать стоимость топлива, необходимое количество топлива и общую стоимость на человека для этой поездки.
Однако важно понимать, что определение точного расстояния между городами может быть сложной задачей. Иногда использование прямой линии (подобной той, которую мы используем в этом калькуляторе) может быть хорошим приближением. Однако оно может оказаться неверным, если ваш маршрут включает обходы, чтобы избежать преград, таких как горы, или проезжать через другие города. В таких случаях рекомендуется использовать онлайн-карты, такие как Google Maps, которые могут рассчитать расстояние в соответствии с фактическим маршрутом, а не просто «в прямой линии».
Наш калькулятор особенно полезен, когда речь идет о измерении расстояний между точками, независимо от пути между ними. Есть и другие сценарии, в которых вас может интересовать расстояние между объектами, а не длина пути, который вы планируете проехать. Например, изучая астрономические объекты, можно измерить расстояние между ними.
Расстояние от Земли до Луны и Солнца - астрономические расстояния
Расстояния в космосе — это концепции, которые могут оказаться настолько далекими и непостижимыми для нашего обыденного восприятия. Рассмотрим два важных астрономических расстояния: от Земли до Луны и от Земли до Солнца.
Расстояние от Земли до Луны:
- Самая ближняя к нам астрономическая соседка — Луна.
- Её расстояние от Земли составляет около 384 000 километров.
Расстояние от Земли до Солнца:
- Наше собственное Солнце находится далеко.
- Расстояние от Земли до Солнца равно приблизительно 150 миллионам километров, что составляет немного более 8 световых минут.
Эти цифры могут показаться огромными, особенно по сравнению с теми расстояниями, которые мы ежедневно преодолеваем на Земле. Например, путешествие из Москвы в Крым, которое обычно занимает около 15 часов, составляет всего ничтожные 1220 километров.
Интересно, что в космосе мы часто измеряем расстояния не в метрах или километрах, а во времени, используя световые годы. Это связано с тем, что расстояния в космосе настолько велики, что геометрические единицы измерения становятся малоприменимыми. Расстояние до нашей ближайшей звезды, Альфа Центавра, составляет 4 световых года. И даже это расстояние кажется мизерным по сравнению с размерами наблюдаемой Вселенной, которые оцениваются в около 46,6 миллиарда световых лет!
Таким образом, изучение космоса не только расширяет наше понимание масштабов, но также заставляет нас пересматривать и переосмысливать понятия расстояния и времени. Это интересный философский и физический аспект, который помогает нам лучше понять Вселенную и её многогранные измерения.
Расстояние за пределы длины
Понятие расстояния, обычно связанное с геометрической длиной, можно расширить, чтобы включить разницу между двумя вещами. Это открывает новые возможности для измерения и выражения расстояния. Давайте рассмотрим несколько способов, как можно интерпретировать расстояние:
Расстояние между числами: Можно измерить расстояние как разницу между двумя числами. Это одномерное расстояние, которое легко вычислить путем вычитания одного числа из другого.
Процентное расстояние: В некоторых случаях полезно измерять расстояние как процентную разницу между величинами. Это может быть более информативным способом сравнения.
Расстояние в других единицах измерения: Расстояние можно измерять в разных единицах, в зависимости от контекста. Например, разница в температуре может быть рассмотрена как расстояние в градусах. Это открывает новые способы сравнения различных величин.
Временное расстояние: Расстояние можно измерять во времени, особенно в случаях, связанных с перемещением. Например, расстояние вождения можно измерить во времени, а не в длине, учитывая среднюю скорость движения.
Расстояние в физике твердого тела: В физике твердого тела расстояние, которое частица проходит между взаимодействиями, может быть измерено средним свободным пробегом. Это связано с длиной и позволяет оценить взаимодействия в материале.
Финансовые расстояния: В финансах расстояние может быть связано с разницей в ценах, например, между текущей и будущей стоимостью актива. Это расстояние может быть влиянием износа, внешних факторов и других переменных.
Этот философский взгляд на расстояния показывает, как разнообразными и абстрактными могут быть понятия расстояния, и как они могут применяться в различных областях. Важно выбирать подходящий способ измерения в каждой конкретной ситуации.
Как найти расстояние между двумя точками?
Чтобы найти расстояние между двумя точками, вы можете воспользоваться следующей формулой:
Расстояние = √[(x₂ — x₁)² + (y₂ — y₁)²]
Давайте разберемся, как это сделать:
- Получите координаты обеих точек в пространстве.
- Вычтите координаты x одной точки из координат x другой точки. Сделайте то же самое для компонентов y.
- Возведите каждый из полученных результатов в квадрат.
- Сложите значения, полученные на предыдущем шаге.
- Найдите квадратный корень из этой суммы.
Если вам кажется, что все эти вычисления слишком сложны, вы также можете воспользоваться калькулятором расстояния для упрощения процесса.
Эта формула позволяет находить расстояние между двумя точками в пространстве, будь то на плоскости или в трехмерном пространстве, и она широко используется в геометрии и физике.
Является ли расстояние вектором?
Расстояние — это скалярная величина, а не вектор. Скаляры описываются только числовым значением и не имеют направления. Расстояние между двумя точками — это просто числовая мера, которая указывает, насколько точки находятся друг от друга, независимо от направления.
С другой стороны, вектор представляет собой величину с определенным направлением и числовым значением. Например, смещение от точки A к точке B — это вектор, который имеет определенное направление и длину, указывающую на расстояние между точками A и B. И важно отметить, что смещение от точки A к точке B не равно смещению от точки B к точке A, потому что векторы учитывают направление.
Таким образом, расстояние и векторы — это разные понятия в математике и физике, и они имеют разные свойства.
Что такое щелчок на расстоянии?
«Щелчок» или «клик» в сленге действительно означает километр, что равно приблизительно 0,62 мили. Этот термин часто используется в военной среде и среди мотоциклистов, а также в некоторых других областях, чтобы указать расстояние. Этот сленговый термин может помочь сократить и облегчить коммуникацию, когда необходимо быстро обозначить расстояния в километрах.
Как найти расстояние вектора?
Векторное расстояние — это его величина или длина. Вот как это сделать:
Если у вас есть компоненты вектора (например, x, y и z):
- Возьмите каждую из компонент и возведите их в квадрат.
- Суммируйте квадраты всех компонентов.
- Найдите квадратный корень из этой суммы.
Это даст вам длину вектора, его величину или расстояние от начальной точки (начала координат) до конечной точки, которую представляет вектор.
Если у вас есть полярное представление вектора, где есть число (величина) и угол, то величина этого вектора будет его расстоянием от начала координат.
Что такое единица расстояния в СИ?
Единицей расстояния в Международной системе единиц (СИ) является метр. Метр (символ: м) определен как длина пути, который проходит свет в вакууме за время 1/299 792 458 секунды. Это точное и фундаментальное определение метра в физической системе единиц СИ, и оно обеспечивает точность измерения расстояний. Метр широко используется для измерения длин, размеров и расстояний в научных и повседневных приложениях.
Чему равно расстояние от a до b?
Для того чтобы вычислить расстояние между точками A и B, вам нужно знать координаты (или векторы) этих точек в соответствии с системой координат, в которой вы работаете. Расстояние между двумя точками можно вычислить с использованием формулы для евклидова расстояния в трехмерном пространстве (если это трехмерное пространство) или аналогичной формулы для двумерного пространства.
Для двумерного пространства (где есть только координаты x и y), формула будет следующей:
Расстояние = √((xB — xA)² + (yB — yA)²)
Для трехмерного пространства (где есть координаты x, y и z), формула будет:
Расстояние = √((xB — xA)² + (yB — yA)² + (zB — zA)²)
Donde:
- (xA, yA, zA) — координаты точки A.
- (xB, yB, zB) — координаты точки B.
Подставьте конкретные значения координат точек A и B в соответствующую формулу, и вы получите расстояние между этими точками.
Какова размерность расстояния?
Размерность расстояния зависит от того, в каком пространстве (двумерном, трехмерном, n-мерном и так далее) мы измеряем расстояние и какие координаты используем.
В двумерном пространстве (например, на плоскости), размерность расстояния равна 1, так как расстояние измеряется только вдоль одной оси (например, по координате x или y).
В трехмерном пространстве (например, в объемном пространстве), размерность расстояния составляет 2, так как расстояние измеряется вдоль двух независимых осей (например, по координатам x, y и z).
В n-мерном пространстве размерность расстояния будет равна (n-1), где n — это количество независимых координатных осей.
Таким образом, размерность расстояния зависит от количества измерительных осей в пространстве, в котором вы проводите измерение.
Световой год — это время или расстояние?
Световой год — это единица измерения расстояния, а не времени. Он представляет собой расстояние, которое свет пройдет в течение одного года в вакууме с его постоянной скоростью, приближенно равной 299 792 458 метров в секунду. Это огромное расстояние, и оно используется для измерения масштабов в космосе, особенно при описании расстояний между звездами и галактиками.
Как найти расстояние через скорость и время?
Чтобы найти расстояние, используя скорость и время, вы можете воспользоваться следующей формулой:
Расстояние (S) = Скорость (V) × Время (t)
Это простая формула, где:
- Расстояние (S) измеряется в метрах (или других единицах длины).
- Скорость (V) измеряется в метрах в секунду (м/с), километрах в час (км/ч), милях в час (миль/ч) или других единицах скорости.
- Время (t) измеряется в секундах (с), часах (ч), минутах (мин) или других единицах времени.
Просто умножьте скорость на время, и вы получите расстояние. Убедитесь, что единицы измерения скорости и времени согласуются, чтобы получить правильный результат в нужных единицах длины.
 Sitio web con 1000 mi útiles herramientas y calculadoras SAS Recursos en línea gratuitos con más de 1000 herramientas y calculadoras SAS. Nuestro sitio ofrece una variedad de servicios que incluyen un constructor de ventanas emergentes, un constructor de widgets, un constructor de tarjetas de visita, un generador de códigos QR, un acortador de enlaces con análisis, así como herramientas de descarga de vídeos y de correspondencia de nombres de dominio.
Sitio web con 1000 mi útiles herramientas y calculadoras SAS Recursos en línea gratuitos con más de 1000 herramientas y calculadoras SAS. Nuestro sitio ofrece una variedad de servicios que incluyen un constructor de ventanas emergentes, un constructor de widgets, un constructor de tarjetas de visita, un generador de códigos QR, un acortador de enlaces con análisis, así como herramientas de descarga de vídeos y de correspondencia de nombres de dominio. 



