Sitio web con 1000 mi útiles herramientas y calculadoras SAS Recursos en línea gratuitos con más de 1000 herramientas y calculadoras SAS. Nuestro sitio ofrece una variedad de servicios que incluyen un constructor de ventanas emergentes, un constructor de widgets, un constructor de tarjetas de visita, un generador de códigos QR, un acortador de enlaces con análisis, así como herramientas de descarga de vídeos y de correspondencia de nombres de dominio. Por favor introduzca las variables A, B y C:
Introduzca valores:
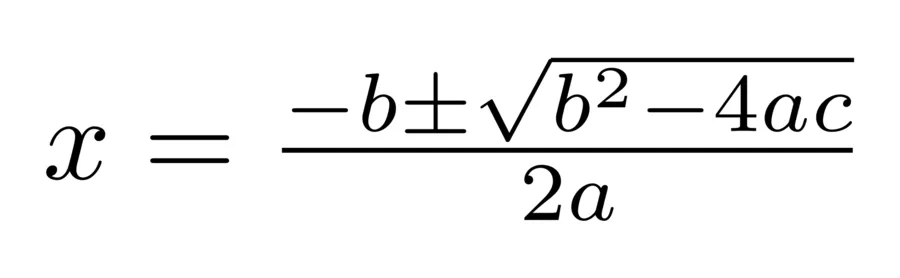
Tabla de contenido
Nuestra calculadora de ecuaciones cuadráticas en línea es una herramienta sencilla y fácil de usar que te ayudará a resolver problemas matemáticos relacionados con ecuaciones cuadráticas. Puedes ingresar fácilmente las probabilidades A, B y C y la calculadora te dará las respuestas a tu pregunta.
¿Cómo funciona? Simplemente ingrese los valores de los coeficientes en los campos correspondientes y nuestra calculadora determinará automáticamente cuántas raíces tiene su ecuación. También explicará qué pasos se realizaron para obtener la respuesta.
Esta calculadora puede resultar útil para cualquiera que encuentre ecuaciones cuadráticas en sus estudios o en su vida cotidiana. Le ayudará a resolver problemas rápida y fácilmente y a comprender las raíces de su ecuación.
Utilice nuestra calculadora de ecuaciones cuadráticas para simplificar su trabajo matemático y obtener una comprensión más profunda de la resolución de ecuaciones. Esta es una herramienta que hará que tus problemas matemáticos sean más accesibles y comprensibles.
Instrucciones para llenar el formulario de la calculadora
Как использовать калькулятор квадратных уравнений:
Переменные A, B и C: В начале формы вы увидите три поля: «A», «B» и «C». Эти переменные представляют собой коэффициенты вашего квадратного уравнения в форме Ax^2 + Bx + C = 0.
Introduzca valores: Для начала решения уравнения, введите значения для каждой из переменных A, B и C в соответствующие поля. Просто щелкните внутри поля и введите число. Если какой-то коэффициент отсутствует, оставьте поле пустым или введите «0».
Resultados: После ввода всех коэффициентов нажмите кнопку «Рассчитать». Наш калькулятор вычислит дискриминант и определит, сколько корней имеет ваше квадратное уравнение.
Área de resultados: Результаты расчета появятся в области под кнопкой «Рассчитать». Здесь вы увидите дискриминант (D), который помогает определить, сколько корней у вашего уравнения. Помимо этого, наш калькулятор предоставит пояснение и объяснение каждого этапа решения уравнения, чтобы сделать процесс более понятным.
Reiniciar: Если вам нужно начать сначала или очистить введенные данные, вы можете нажать кнопку «Сброс». Это позволит вам начать новый расчет.
С помощью нашего калькулятора квадратных уравнений, вы можете легко и быстро решать математические задачи и получать подробные объяснения к каждому этапу расчета. Этот инструмент поможет вам лучше понять процесс решения квадратных уравнений и упростит вашу математическую работу.
¿Para quién es útil esta calculadora?
Данный калькулятор квадратных уравнений полезен для широкого круга людей, включая:
Учащиеся и студенты: Калькулятор помогает ученикам и студентам в решении задач и понимании процесса решения квадратных уравнений, что может быть полезным при обучении математике.
Преподаватели: Преподаватели могут использовать калькулятор как учебный инструмент для демонстрации решения квадратных уравнений и объяснения математических концепций.
Самоучители: Люди, самостоятельно изучающие математику, могут использовать калькулятор для проверки своих расчетов и углубления в изучение квадратных уравнений.
Работники в области науки и инженерии: Калькулятор может быть полезным инструментом для профессионалов, которые сталкиваются с квадратными уравнениями в своей работе, таким как инженеры и физики.
Люди, решающие практические задачи: Любой, кто сталкивается с задачами, которые можно сформулировать в виде квадратных уравнений, может воспользоваться калькулятором для быстрого расчета и получения ответов.
Родители и опекуны: Родители могут помочь своим детям с домашними заданиями по математике, используя этот калькулятор как образовательный ресурс.
Все, кто нуждается в решении квадратных уравнений: Калькулятор доступен всем, кому нужно решать квадратные уравнения в повседневной жизни, будь то для финансовых расчетов, строительства или других практических задач.
Калькулятор квадратных уравнений предоставляет удобный способ решения математических задач и понимания процесса решения, делая математику более доступной и понятной для широкой аудитории.
Ejemplos y cálculos usando esta calculadora.
Давайте рассмотрим несколько примеров решения квадратных уравнений с использованием нашего калькулятора:
Ejemplo 1: Решение уравнения с дискриминантом больше нуля.
У нас есть уравнение: 2x^2 + 3x - 2 = 0
Введите значения коэффициентов в соответствующие поля: A = 2, B = 3, C = -2.
Haga clic en el botón "Calcular".
Resultado:
- Дискриминант (D) равен 25 (положительное значение).
- Калькулятор показывает, что у уравнения есть два корня.
- Первый корень (x1) равен -2.
- Второй корень (x2) равен 1.
Таким образом, решение уравнения 2x^2 + 3x - 2 = 0 — это два корня: x1 = -2 и x2 = 1.
Ejemplo 2: Решение уравнения с дискриминантом равным нулю.
У нас есть уравнение: x^2 - 4x + 4 = 0
Введите значения коэффициентов в соответствующие поля: A = 1, B = -4, C = 4.
Haga clic en el botón "Calcular".
Resultado:
- Дискриминант (D) равен 0.
- Калькулятор показывает, что у уравнения есть один корень (двойной корень).
- Корень (x1) и второй корень (x2) равны 2.
Это означает, что решение уравнения x^2 - 4x + 4 = 0 — это один корень (двойной корень) x1 = x2 = 2.
Пример 3: Решение уравнения с отрицательным дискриминантом.
У нас есть уравнение: 3x^2 + 2x + 1 = 0
Введите значения коэффициентов в соответствующие поля: A = 3, B = 2, C = 1.
Haga clic en el botón "Calcular".
Resultado:
- Дискриминант (D) равен -8 (отрицательное значение).
- Калькулятор показывает, что у уравнения нет действительных корней в множестве действительных чисел (R).
Таким образом, решение уравнения 3x^2 + 2x + 1 = 0 — это отсутствие действительных корней (решений) в множестве действительных чисел.
Объяснение теории квадратных уравнений
Квадратное уравнение — это математическое уравнение специального вида, в котором степень неизвестной переменной (обычно обозначаемой как «x») равна двум. Квадратные уравнения имеют общий вид:
Ax^2 + Bx + C = 0
Donde:
- «A», «B» и «C» — это коэффициенты, которые могут быть любыми действительными числами, причем «A» не должно быть равным нулю (A ≠ 0).
- «x» — неизвестная переменная, которую мы пытаемся найти.
- «0» — это правая часть уравнения, означающая, что уравнение равно нулю.
Такие уравнения называются «квадратными» из-за присутствия переменной «x» во второй степени (x^2). Квадратные уравнения могут иметь разное количество корней в зависимости от значения их дискриминанта (D), который вычисляется по формуле:
D = B^2 — 4AC
Определение количества корней на основе дискриминанта:
- Если D > 0, то уравнение имеет два различных действительных корня.
- Если D = 0, то уравнение имеет один действительный корень (двойной корень).
- Если D < 0, то уравнение не имеет действительных корней (корни комплексные).
Когда D больше нуля, уравнение имеет два различных решения, которые могут быть положительными или отрицательными. Если D равно нулю, то уравнение имеет один корень, который также называется «двойным корнем», и этот корень будет равен -B / (2A). Когда D меньше нуля, уравнение не имеет действительных корней, и его решения будут комплексными числами.
Квадратные уравнения широко используются в различных областях математики и наук, а также в практических задачах, таких как физика, инженерия и финансы, для моделирования и анализа различных явлений и процессов.
Примеры уравнений и их решение
Давайте рассмотрим несколько примеров квадратных уравнений и решим их с использованием нашего калькулятора:
Ejemplo 1: Решение уравнения с положительным дискриминантом.
Уравнение: 2x^2 — 5x + 2 = 0
Введите значения коэффициентов в соответствующие поля: A = 2, B = -5, C = 2.
Haga clic en el botón "Calcular".
Resultado:
- Дискриминант (D) равен 25 (положительное значение).
- Калькулятор показывает, что у уравнения есть два корня.
- Первый корень (x1) равен 2.
- Второй корень (x2) равен 0.5.
Таким образом, решение уравнения 2x^2 — 5x + 2 = 0 — это два корня: x1 = 2 и x2 = 0.5.
Ejemplo 2: Решение уравнения с нулевым дискриминантом.
Уравнение: x^2 — 4x + 4 = 0
Введите значения коэффициентов в соответствующие поля: A = 1, B = -4, C = 4.
Haga clic en el botón "Calcular".
Resultado:
- Дискриминант (D) равен 0.
- Калькулятор показывает, что у уравнения есть один корень (двойной корень).
- Корень (x1) и второй корень (x2) равны 2.
Это означает, что решение уравнения x^2 — 4x + 4 = 0 — это один корень (двойной корень) x1 = x2 = 2.
Пример 3: Решение уравнения с отрицательным дискриминантом.
Уравнение: 3x^2 + x + 2 = 0
Введите значения коэффициентов в соответствующие поля: A = 3, B = 1, C = 2.
Haga clic en el botón "Calcular".
Resultado:
- Дискриминант (D) равен -23 (отрицательное значение).
- Калькулятор показывает, что у уравнения нет действительных корней в множестве действительных чисел (R).
Таким образом, решение уравнения 3x^2 + x + 2 = 0 — это отсутствие действительных корней (решений) в множестве действительных чисел.
Таблица с формулами и коэффициентами
Таблица с формулами и коэффициентами для расчета дискриминанта (D) и корней квадратных уравнений:
| Тип уравнения | Общий вид | Формула для дискриминанта (D) | Формулы для корней (x1 и x2) |
|---|---|---|---|
| Ecuación cuadrática | Ax^2 + Bx + C = 0 | D = B^2 — 4AC | x1 = (-B + √D) / (2A) <br> x2 = (-B — √D) / (2A) |
| Уравнение с положительным D | 2x^2 — 3x — 2 = 0 | D = 3^2 — 4 * 2 * (-2) | x1 = (3 + √25) / 4 x1 = 2.5 <br> x2 = (3 — √25) / 4 x2 = -0.5 |
| Уравнение с нулевым D | x^2 — 4x + 4 = 0 | D = (-4)^2 — 4 * 1 * 4 | x1 = (-(-4) + √0) / (2 * 1) x1 = 2 <br> x2 = (-(-4) — √0) / (2 * 1) x2 = 2 |
| Уравнение с отрицательным D | 3x^2 + x + 2 = 0 | D = 1^2 — 4 * 3 * 2 | x1 = (-1 + √-23) / (2 * 3) x1 = (-1 + √-23) / 6 x1 ≈ 0.33 <br> x2 = (-1 — √-23) / (2 * 3) x2 = (-1 — √-23) / 6 x2 ≈ -1.67 |
Эта таблица поможет вам понять, как вычислять дискриминант (D) и корни (x1 и x2) для различных квадратных уравнений, в зависимости от их коэффициентов.
Применение квадратных уравнений в реальной жизни
Квадратные уравнения имеют множество практических применений в различных областях жизни. Вот несколько примеров:
Физика: В физике квадратные уравнения используются для моделирования различных физических явлений. Например, при расчете траектории броска предмета под углом к горизонту, можно использовать квадратное уравнение для определения момента падения предмета.
Инженерия: Инженеры используют квадратные уравнения при проектировании механических систем, таких как мосты и здания. Они могут использовать уравнения для определения распределения нагрузки и прочности материалов.
Финансы: Квадратные уравнения могут использоваться в финансовых расчетах. Например, при определении стоимости опций на акции и облигации.
Экономика: В экономике квадратные уравнения могут быть использованы для анализа зависимости между спросом и предложением на рынке. Они также могут быть использованы для прогнозирования экономических показателей.
Геометрия: В геометрии квадратные уравнения могут быть использованы для определения формы и положения геометрических фигур. Например, уравнение окружности имеет квадратную форму.
Медицина: В медицинских исследованиях квадратные уравнения могут использоваться для анализа данных и моделирования биологических процессов.
Информационные технологии: В компьютерной графике и компьютерной анимации квадратные уравнения используются для создания плавных движений и анимации объектов.
Архитектура: Архитекторы могут использовать квадратные уравнения для проектирования архитектурных элементов, таких как арки и купола.
Это всего лишь несколько примеров того, как квадратные уравнения находят применение в реальной жизни. Они являются мощным инструментом для моделирования и анализа различных явлений и процессов в разных областях знаний.
