Die potentielle Gravitationsenergie ist gleich:
Berechnungshistorie:
Inhaltsverzeichnis
Der Gravitational Potential Energy (GPE)-Rechner ist ein einfaches und praktisches Werkzeug zur Berechnung der Energie, die ein Objekt unter dem Einfluss der Schwerkraft ansammelt. Mit diesem Rechner können Sie ermitteln, wie viel Energie ein Objekt hat, wenn es eine bestimmte Höhe erreicht oder in einem Gravitationsfeld aufsteigt.
Hauptvorteile des Rechners:
- Benutzerfreundlichkeit: Geben Sie einfach die Masse des Objekts und die Höhe ein, bis zu der es steigt.
- Einheiten: Sie können die von Ihnen bevorzugten Einheiten für Gewicht und Größe auswählen, z. B. Kilogramm oder Pfund für das Gewicht und Meter oder Fuß für die Größe.
- Berechnungsverlauf: Der Rechner speichert einen Verlauf aller Ihrer Berechnungen, sodass Sie diese anzeigen, kopieren und sogar zur späteren Verwendung herunterladen können.
- Klare Ergebnisse: Das Berechnungsergebnis wird in einer einfachen, für jedermann verständlichen Form dargestellt.
Dieser Rechner ist nützlich für Studenten, Studenten und alle, die sich für Physik oder Ingenieurwesen interessieren. Damit können Sie ganz einfach die potenzielle Gravitationsenergie bestimmen und diese in Ihren Problemen und Berechnungen verwenden.
Anleitung zum Ausfüllen des Rechnerformulars
Калькулятор Гравитационной Потенциальной Энергии (ГПЭ) предоставляет вам возможность легко и точно рассчитать ГПЭ объекта. Ниже приведена подробная инструкция по заполнению формы калькулятора:
Masse:
- Это поле предназначено для ввода массы объекта, который вы хотите проанализировать.
- Вы можете использовать любые удобные вам единицы измерения, такие как килограммы (кг) или фунты (lbs). Выберите соответствующую единицу из выпадающего списка.
- Например, если ваш объект весит 10 килограммов, введите «10» в поле «Масса» и выберите «кг» из списка.
Höhe:
- В это поле следует ввести высоту, на которую поднимается объект или на которую вы хотите рассчитать ГПЭ.
- Также, как и с массой, вы можете выбрать единицы измерения высоты, такие как метры (м) или футы (ft), из выпадающего списка.
- Например, если объект поднимается на высоту в 5 метров, введите «5» в поле «Высота» и выберите «м» из списка.
Кнопка «Рассчитать GPE»:
- После заполнения полей «Масса» и «Высота», нажмите на эту кнопку для выполнения расчета.
- Результат расчета ГПЭ будет отображен под кнопкой и будет выражен в джоулях (Дж).
Berechnungshistorie:
- Ниже результатов расчета есть раздел «История вычислений», где отображаются результаты всех предыдущих расчетов.
- Вы можете просматривать, копировать и скачивать историю вычислений с помощью соответствующих кнопок «Скопировать историю» и «Скачать историю».
Очистить историю:
- Кнопка «Очистить историю» позволяет удалить все предыдущие записи из истории вычислений, начиная с чистого листа.
Теперь вы готовы использовать калькулятор ГПЭ для своих расчетов. Введите массу и высоту объекта, нажмите «Рассчитать GPE», и результат будет доступен вам сразу же. И не забудьте, что у вас всегда есть доступ к истории вычислений для удобства отслеживания предыдущих результатов.
Für wen ist dieser Rechner nützlich?
Данный калькулятор гравитационной потенциальной энергии (ГПЭ) может быть полезен различным группам пользователей в зависимости от их интересов и потребностей. Вот несколько категорий пользователей, которым может быть полезен этот калькулятор:
Студентам и ученикам:
- Калькулятор поможет студентам и школьникам изучать и понимать концепцию ГПЭ в рамках учебных курсов по физике.
- Он может быть полезен для выполнения учебных заданий и расчетов, связанных с гравитацией.
Преподавателям и учителям:
- Преподаватели могут использовать этот калькулятор для демонстрации и объяснения концепции ГПЭ во время уроков.
- Он может быть включен в учебные материалы и рекомендован студентам для самостоятельных исследований.
Инженерам и научным работникам:
- Профессионалы в области инженерии и науки могут использовать калькулятор для выполнения точных расчетов в рамках своей работы.
- ГПЭ имеет широкое применение в различных инженерных и научных областях, таких как строительство, астрономия и геология.
Любителям физики и науки:
- Любители физики и науки могут использовать калькулятор для более глубокого понимания принципов гравитации и потенциальной энергии.
- Он позволяет проводить интересные эксперименты и расчеты в домашних условиях.
Инженерам-строителям:
- Инженеры, занимающиеся проектированием и строительством, могут использовать калькулятор для расчета ГПЭ при проектировании различных инженерных сооружений, таких как мосты и дамбы.
Энтузиастам и любознательным людям:
- Калькулятор может быть интересен для всех, кто хочет углубиться в мир науки и физики, а также для тех, кто просто интересуется темой гравитации и потенциальной энергии.
В целом, данный калькулятор ГПЭ доступен широкой аудитории и может быть полезным для образовательных, учебных и профессиональных целей, а также для чистого научного исследования и удовлетворения научного любопытства.
Что такое ГПЭ
Гравитационная потенциальная энергия (ГПЭ) — это форма потенциальной энергии, которую обладает объект, находясь в поле гравитации. Простыми словами, это количество энергии, которое объект может получить, если его поднять вверх против силы притяжения Земли. ГПЭ зависит от массы объекта, высоты, на которую его подняли, и ускорения свободного падения (обычно принимается за около 9.81 метра в секунду в квадрате на поверхности Земли).
В повседневной жизни ГПЭ имеет большое значение. Вот несколько примеров:
Энергоснабжение: ГПЭ используется в гидроэлектростанциях, где вода поднимается вверх к высокому резервуару, а затем опускается, преобразуя ГПЭ в электроэнергию. Это способствует производству электроэнергии, которая питает наши дома и предприятия.
Transport: Поднимая автомобиль на подъемник в автомастерской или поднимая груз на кране, мы также работаем с ГПЭ. Расчет ГПЭ может быть полезным при определении, сколько энергии необходимо для поднятия или перемещения объектов.
Спорт: В спорте, таком как прыжки и метания, ГПЭ влияет на высоту, на которую можно подняться или дальность броска. Понимание ГПЭ может помочь спортсменам улучшить свои результаты.
Исследования и инженерия: В науке и инженерии ГПЭ играет важную роль при проектировании и анализе различных систем, таких как ракеты, мосты и сооружения.
Мы все интуитивно понимаем, что поднятие тяжелого груза над головой может быть опасным. Однако опасность не всегда связана с весом самого груза, а скорее с тем, как хорошо он закреплен. Нас волнует то, что сила, удерживающая груз от падения под действием гравитации, может внезапно перестать действовать. Если говорить более точно с физической точки зрения, нас интересует гравитационная потенциальная энергия этого груза.
Важно отметить, что все консервативные силы связаны с потенциальной энергией. Сила гравитации здесь не исключение. Гравитационной потенциальной энергии обычно присваивается символ U_g. Этот символ описывает потенциальную энергию, которую объект обладает благодаря своему положению в гравитационном поле.
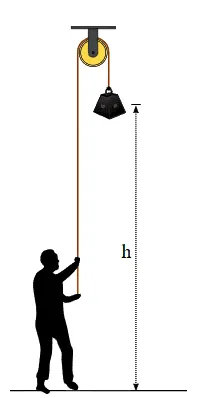
Давайте рассмотрим ситуацию, когда у нас есть объект массой «m», который мы поднимаем на высоту «h» против силы тяжести. Объект движется вертикально, поднимаясь с помощью шкива и веревки, поэтому сила, противодействующая гравитации (F_g), и сила тяжести направлены в одном направлении. Если «g» — ускорение свободного падения, то работу, которую сила, противодействующая гравитации, выполняет над объектом, можно найти, умножив величину силы тяжести (F_g) на расстояние, на которое объект поднят (h). Это предполагает, что ускорение свободного падения остается постоянным на протяжении всей высоты «h».
Уравнение для гравитационной потенциальной энергии (U_g) выглядит следующим образом:
U_g = F_g * h = m * g * h
Когда объект поднимается вертикально, он приобретает гравитационную потенциальную энергию. Если бы сила, удерживающая объект, исчезла, объект начал бы падать обратно на землю, и его потенциальная энергия превратилась бы в кинетическую энергию движущегося объекта. Наша статья о законе сохранения энергии включает в себя несколько примеров, которые можно решить, понимая, как гравитационная потенциальная энергия преобразуется в другие формы энергии.
Интересно, что в гравитационной потенциальной энергии можно выбрать произвольный нулевой уровень. Другими словами, мы можем выбрать любую вертикальную точку, где «h=0», и считать ее нулевым уровнем. Для простых механических задач удобно выбрать нулевым уровнем пола лаборатории или поверхности стола. Однако в принципе мы могли бы выбрать любую другую точку, которую называем исходной. Гравитационная потенциальная энергия также может быть отрицательной, если объект находится ниже нулевого уровня. Главное — использовать одну и ту же точку отсчета во всех вычислениях.
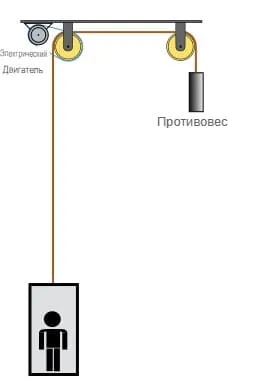
Упражнение 1а. Сколько электроэнергии потребует лифт, чтобы поднять человека весом 75 кг на высоту 50 метров, если эффективность лифтовой системы составляет 25 %? Предположим, что масса пустой кабины лифта уравновешена противовесом.
Для рассчета затрат электроэнергии необходимо использовать следующую формулу: Электроэнергия = работа / эффективность.
Wo:
- Работа = масса * ускорение свободного падения * высота.
- Масса человека = 75 кг.
- Ускорение свободного падения ≈ 9.81 м/с².
- Высота подъема = 50 м.
Теперь мы можем рассчитать работу и затраты электроэнергии: Работа = 75 кг * 9.81 м/с² * 50 м = 36842.5 Дж (джоулей).
Теперь рассчитаем затраты электроэнергии: Электроэнергия = 36842.5 Дж / 0.25 (эффективность) = 147370 Дж (джоулей).
Упражнение 1b (дополнение): Какова будет стоимость поездки на лифте, если предположить, что стоимость электроэнергии составляет 0.10 рубля за кВт⋅час.
Для рассчета стоимости электроэнергии, нам нужно преобразовать Джоули в кВт⋅час. 1 Дж = 2.77778e-7 кВт⋅час.
Электроэнергия в кВт⋅час = 147370 Дж * 2.77778e-7 кВт⋅час/Дж = 0.041 кВт⋅час.
Теперь рассчитаем стоимость: Стоимость = 0.041 кВт⋅час * 0.10 рубля/кВт⋅час = 0.0041 рубля.
Упражнение 2. Гравитационная потенциальная энергия — одна из немногих форм энергии, которую можно эффективно использовать для хранения в больших масштабах. Для накопления избыточной электроэнергии от ветряных и солнечных источников необходимы масштабные системы хранения, которые могут передавать энергию в сеть во время пикового спроса. Гидроаккумулирующие системы могут достичь этой цели.
На изображении ниже показан пример такой системы. Вода поднимается в верхний резервуар, используя избыточную энергию для запуска двигателя, который активирует турбинный насос. Когда потребность в энергии высока, направление потока меняется. Насос становится генератором, приводимым в действие гравитационной потенциальной энергией воды в верхнем резервуаре. Вода может быть выпущена очень быстро, чтобы удовлетворить пиковые потребности в электроэнергии для всего города или даже нескольких городов.
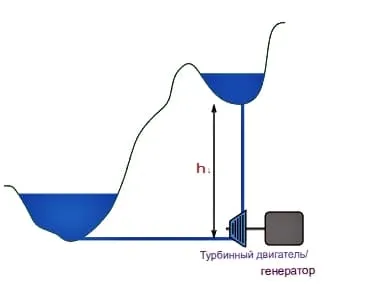
Гидроаккумулирующая станция округа Бат является крупнейшей в мире гидроаккумулирующей системой. Она обслуживает 60 миллионов человек и имеет генерирующую мощность около 3 гигаватт (3 ГВт). Перепад высоты системы составляет 380 метров. Предположим, что общая эффективность системы составляет 80%. Теперь мы можем рассчитать, какой объем воды из верхнего резервуара должен пройти через турбину за 30 минут, чтобы обеспечить поставку 3 ГВт электроэнергии в город.
Для расчета объема воды используем следующую формулу:
Объем воды = Электроэнергия / (плотность * g * h * эффективность).
Wo:
- Электроэнергия = 3 ГВт = 3 * 10^9 Вт.
- Плотность воды ≈ 1000 кг/м³.
- g (ускорение свободного падения) ≈ 9.81 м/с².
- h (высота) = 380 м.
- Эффективность системы = 80%.
Теперь выполним расчет:
Объем воды = (3 * 10^9 Вт) / (1000 кг/м³ * 9.81 м/с² * 380 м * 0.80) ≈ 122292 м³.
Таким образом, для обеспечения поставки 3 ГВт электроэнергии в город за 30 минут, необходимо, чтобы примерно 122292 м³ воды прошли через турбину.
Таблица физических констант
Таблица основных физических констант, которые могут быть полезными для различных физических расчетов:
| Физическая константа | Значение (приближенное) | Einheiten |
|---|---|---|
| Ускорение свободного падения (гравитация) | 9.81 м/с² | метры в секунду в квадрате |
| Скорость света в вакууме | 299,792,458 м/с | метры в секунду |
| Постоянная Планка (h) | 6.62607015 x 10^-34 Дж·с | джоули в секунду |
| Элементарный заряд (e) | 1.602176634 x 10^-19 Кл | кулоны |
| Масса электрона | 9.10938356 x 10^-31 кг | килограммы |
| Масса протона | 1.6726219 x 10^-27 кг | килограммы |
| Постоянная газовых постоянных (R) | 8.314462618 Дж/(моль·К) | джоули / (моль·кельвин) |
| Постоянная Больцмана (k) | 1.380649 x 10^-23 Дж/К | джоули / кельвин |
| Постоянная тяготения (G) | 6.67430 x 10^-11 м³/(кг·с²) | метры³ / (килограмм·секунда²) |
Помните, что значения этих констант могут использоваться в различных физических формулах для проведения различных расчетов и анализа явлений в мире физики.
Заголовок аккордеона
Как работает гравитация, когда поле неоднородно?
Когда мы рассматриваем задачи, связанные с большими расстояниями, мы не можем считать гравитационное поле равномерным. Давайте вспомним закон всемирного тяготения Ньютона, который говорит о том, что сила притяжения между двумя массами, обозначим их как m₁ и m₂, уменьшается с квадратом расстояния между ними, обозначим это расстояние как r. Гравитационная постоянная обозначается как G.
Итак, формула для этой силы выглядит так:
F = (G * m₁ * m₂) / r²
Здесь F — сила притяжения, G — гравитационная постоянная, m₁ и m₂ — массы двух объектов, а r — расстояние между ними в квадрате.
Когда мы имеем дело с гравитационной потенциальной энергией на больших расстояниях, мы обычно выбираем точку бесконечности как нашу нулевую точку потенциальной энергии. Это может показаться странным, так как все значения гравитационной потенциальной энергии становятся отрицательными.
Это имеет смысл, так как по мере увеличения расстояния r сила гравитации стремится к нулю. Только когда r становится бесконечно большим, мы можем считать, что гравитационная потенциальная энергия близка к нулю.
Для космического корабля, покидающего Землю, это происходит на высоте около 5 * 10^7 метров над поверхностью, что примерно в четыре раза больше диаметра Земли. На этой высоте ускорение свободного падения уменьшилось примерно до 1% от значения на поверхности.
Если мы учитываем, что проделанная работа равна силе, умноженной на расстояние, то мы видим, что умножение силы гравитации на расстояние r уменьшает квадрат в знаменателе.
Поэтому, если мы устанавливаем нулевую потенциальную энергию на бесконечности, гравитационная потенциальная энергия U_g как функция r равна:
U_g(r) = — (G * m₁ * m₂) / r
Это удобно для расчета энергии, необходимой для перемещения между разными телами в Солнечной системе. Это также позволяет представить гравитационную яму, из которой нужно «вылезти», чтобы перейти с одной планеты на другую.
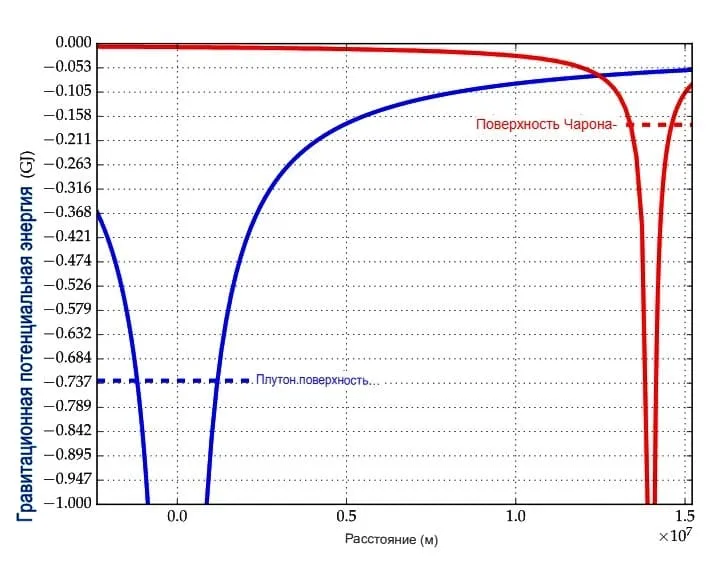
На изображении ниже показаны гравитационные ямы Плутона и его спутника Харона, калиброванные для космического корабля массой 1000 кг.
Основываясь на графике, показанном на изображении выше, определите, какую работу необходимо совершить против силы тяжести в путешествии, начавшемся в состоянии покоя на поверхности Харона и прибывшем на поверхность Плутона с нулевой скоростью?
 SAS-Tools-Site mit Tausenden nützlichen SAS-Tools und Rechnern
SAS-Tools-Site mit Tausenden nützlichen SAS-Tools und Rechnern