Введите частоту от
Введите частоту
Преобразованная частота
textDesc
Справочная формула
refDesc
Оглавление
Онлайн-конвертер частоты — это удобный инструмент, который поможет вам легко пересчитать частоту из одних единиц измерения в другие. Если вы когда-либо сталкивались с частотой и хотели бы перевести ее из одной формы в другую, этот конвертер сделает это быстро и просто.
На главной странице вы увидите два поля для ввода частоты — одно для исходных значений, а другое для желаемых результатов. Выберите единицы измерения из выпадающего списка, чтобы указать, в какой форме вы хотите видеть результат.
Когда вы введете начальное значение и выберете единицы измерения, конвертер автоматически выполнит вычисления и покажет вам преобразованный результат. Это простой способ получить нужную информацию без необходимости проводить сложные расчеты.
Кроме того, на этой странице вы найдете справочную информацию о частоте и о том, как проводятся вычисления. Это может быть полезным, если вы хотите лучше понять, как работает процесс конвертации.
Описание единиц измерения частоты
Давайте рассмотрим различные единицы измерения частоты и их применение:
Герц (Hz):
- Обозначение: Hz
- Применение: Герцы — это стандартная единица измерения частоты, которая используется для измерения количества циклов (или вибраций) в секунду. Она широко применяется в физике, инженерии и электронике для описания частоты сигналов и колебаний.
Килогерц (kHz):
- Обозначение: kHz
- Применение: Килогерцы представляют собой тысячи герц и обычно используются в высокочастотных приложениях, таких как радиовещание, телевизионное вещание и связь. Также они часто встречаются в области медицинской диагностики и измерения частоты процессоров.
Мегагерц (MHz):
- Обозначение: MHz
- Применение: Мегагерцы равны миллиону герц и применяются в более высокочастотных системах, таких как микроволны, сотовая связь, беспроводные сети и радиоизлучение.
RPM (обороты в минуту):
- Обозначение: RPM
- Применение: Эта единица измерения используется для определения скорости вращения механических устройств, таких как двигатели, колеса, вентиляторы и многие другие. Она широко применяется в автомобильной промышленности, а также в производстве и строительстве.
Обороты в секунду (rps):
- Обозначение: rps
- Применение: Обороты в секунду измеряют скорость вращения, но в более быстром формате — в оборотах в секунду. Эта единица может использоваться, например, для определения частоты вращения мелких механических устройств или двигателей.
Радианы в секунду (rads):
- Обозначение: rads
- Применение: Радианы в секунду измеряют скорость изменения угла. Они часто используются в физике и инженерии при рассмотрении вращательных движений, таких как вращение колеса автомобиля или вентилятора.
Радианы в минуту (radm):
- Обозначение: radm
- Применение: Эта единица измерения также относится к скорости изменения угла, но выражается в радианах в минуту. Она может использоваться при изучении медленных вращательных движений и угловых скоростей.
Каждая из этих единиц измерения имеет свое собственное применение в различных областях науки, техники и производства, что делает их важными инструментами для измерения и анализа различных физических явлений и процессов.
Где и как используется конвертация частоты в разных областях
Конвертация частоты имеет важное значение во множестве областей и применяется для различных целей. Вот несколько примеров реальных сценариев использования в различных отраслях:
Телекоммуникации:
- Пример: Мобильные сети, такие как 4G и 5G, используют конвертацию частоты для передачи данных между базовыми станциями и мобильными устройствами. Разные диапазоны частот используются для разных целей, например, для передачи голоса или данных.
Медицина:
- Пример: В медицинских оборудованиях, таких как УЗИ (ультразвуковое исследование), конвертация частоты используется для создания изображений внутренних органов пациента. Высокочастотные звуковые волны преобразуются в низкочастотные сигналы для визуализации.
Музыкальная индустрия:
- Пример: В аудиоэффектах и синтезаторах звука частота звуковых волн может быть конвертирована для создания различных музыкальных эффектов, таких как изменение тональности или скорости воспроизведения.
Радиоэлектроника:
- Пример: Радиолокационные системы и радиосвязь часто используют конвертацию частоты для переноса информации или обнаружения объектов. Преобразование частоты позволяет радиосигналам путешествовать на большие расстояния и проникать через различные среды.
Промышленность:
- Пример: В производственных процессах, таких как контроль скорости вращения двигателей или механических систем, часто используется конвертация частоты. Например, регулирование скорости конвейера в заводе может осуществляться путем изменения частоты вращения моторов.
Авиация:
- Пример: В авиации конвертация частоты используется для навигации и связи. Радиосигналы могут быть преобразованы для точной определения положения и безопасной коммуникации между летательными аппаратами и землей.
Научные исследования:
- Пример: В физических экспериментах и лабораторных исследованиях частота может быть конвертирована для измерения и анализа различных явлений, таких как акустические и электромагнитные волны.
Конвертация частоты является ключевой техникой во многих областях и позволяет адаптировать сигналы для различных задач, обеспечивая эффективность и точность в разнообразных приложениях.
Технические характеристики устройств, которые измеряют или используют частоту
Когда речь идет о технических характеристиках устройств, связанных с измерением или использованием частоты, есть несколько ключевых параметров и зависимостей, которые важно учитывать:
Осциллографы:
- Частотный диапазон: Этот параметр определяет, в каких пределах частот осциллограф способен измерять и отображать сигналы. Например, осциллограф с частотным диапазоном 100 МГц может измерять сигналы частотой до 100 мегагерц.
- Чувствительность: Это показатель, который указывает, какие минимальные амплитуды сигналов могут быть обнаружены осциллографом при определенной частоте. Большая чувствительность позволяет измерять слабые сигналы.
Радиоаппаратура:
- Частотный диапазон: Эта характеристика указывает, в каких диапазонах частот работает радиоаппаратура. Например, радио может работать на частотах от 88 до 108 МГц для FM-диапазона.
- Выбор частоты: В радиоаппаратуре пользователь может выбирать частоту для настройки на определенный радиостанции или сигнал. Это позволяет слушать разные радиостанции на разных частотах.
Звуковые системы:
- Частотный диапазон динамиков: Этот параметр определяет, какие частоты звуковые системы способны воспроизводить. Например, динамик может иметь частотный диапазон от 20 Гц до 20 кГц, что соответствует слышимому спектру человеческого уха.
- Частотная характеристика: Это графическое представление, которое показывает, как усиление звуковой системы изменяется в зависимости от частоты. Эта характеристика важна для того, чтобы определить, как хорошо система воспроизводит разные частоты.
Частота играет критическую роль в работе этих устройств. Например, в звуковых системах важно, чтобы динамики могли воспроизводить нужные звуковые частоты для достижения качественного звучания. В радиоаппаратуре и осциллографах частота определяет, какие сигналы могут быть обработаны или измерены. Таким образом, понимание и учет частотных характеристик является важным аспектом при выборе и настройке этих устройств.
Таблица сравнения различных частот
Таблица сравнения различных единиц измерения частоты:
| Единица измерения | Обозначение | Эквивалент в Герцах (Hz) |
|---|---|---|
| Герц (Hz) | Hz | 1 Hz |
| Килогерц (kHz) | kHz | 1,000 Hz (1 kHz = 10^3 Hz) |
| Мегагерц (MHz) | MHz | 1,000,000 Hz (1 MHz = 10^6 Hz) |
| RPM (обороты/мин) | RPM | Варьируется в зависимости от устройства |
| Оборотов/сек | rps | Варьируется в зависимости от устройства |
| Радиан/сек | rads | Варьируется в зависимости от устройства |
| Радиан/мин | radm | Варьируется в зависимости от устройства |
Эта таблица позволяет вам сравнивать разные единицы измерения частоты и видеть их эквиваленты в Герцах для лучшего понимания и преобразования значений.
Определение частоты и формула частоты
Давайте разберемся с определением частоты и связанной с ней формулой, используя простые слова и структурированное объяснение.
Частота — это сколько раз что-то происходит в секунду. Если представить волну на воде, то частота скажет нам, сколько волн проходит через одну точку за одну секунду.
Простейшая формула для вычисления частоты выглядит так:
Частота (f) = 1 / Период (T)
Здесь f обозначает частоту, а T обозначает время, которое нужно для завершения одного цикла волны, измеряемое в секундах.
В международной системе единиц (СИ), частоту измеряют в герцах (Гц), что означает одну волну в секунду. Есть и другие единицы измерения частоты, такие как миллигерц (мГц), килогерц (кГц), мегагерц (МГц), гигагерц (ГГц) и терагерц (ТГц), которые используются в зависимости от масштаба частоты.
Частотное уравнение от длины волны
Давайте углубимся в понимание связи между частотой, длиной волны и скоростью распространения волн.
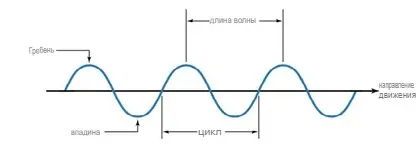
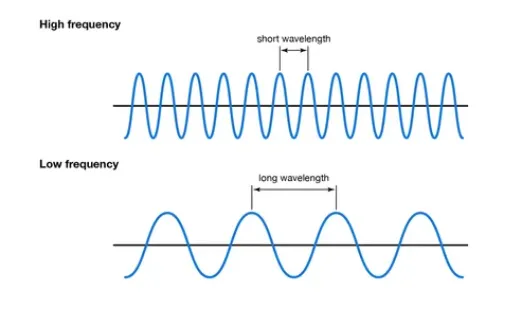
Длина волны — это просто расстояние между соседними гребнями или впадинами волны. С другими словами, это длина одного волнового цикла. Если длина волны больше, то частота будет меньше, и наоборот.
Кроме того, скорость, с которой волна движется, определяет, сколько волн проходит через определенную точку в секунду. Если скорость волны выше, то и частота тоже будет выше.
С учетом этих двух соотношений мы можем получить следующее уравнение для частоты:
Частота (f) = Скорость (v) / Длина волны (λ)
Это уравнение показывает, как частота связана с длиной волны и скоростью распространения волн. Если вы знаете скорость и длину волны, вы можете легко вычислить частоту, и наоборот.
Как рассчитать частоту по периоду?
Давайте разберемся, как рассчитать частоту по известному периоду, используя простые примеры.
Пример 1:
Предположим, что у нас есть волна, и один цикл этой волны завершается за 0,25 секунды. Чтобы найти частоту, мы используем частотное уравнение:
Частота (f) = 1 / Период (T)
Теперь подставим значение периода:
f = 1 / 0.25 сек
Далее, мы можем упростить выражение:
f = 4 * 1/сек
И теперь переведем «1/сек» в единицу измерения частоты:
f = 4 Гц (герцы)
Итак, частота этой волны составляет 4 герца.
Пример 2:
Допустим, что волна завершает 360 циклов за 1 минуту. Сначала переведем 1 минуту в секунды, так как частота измеряется в герцах (в секундах):
1 минута = 60 секунд
Теперь используем частотное уравнение:
Частота (f) = Количество циклов / Период (T)
f = 360 / 60 секунд
Далее, упростим выражение:
f = 6/сек
И снова переведем «1/сек» в единицу измерения частоты:
f = 6 Гц (герцы)
Таким образом, частота этой волны составляет 6 герцов.
Как найти частоту волны?
Для расчета частоты волны, когда известны скорость волны и длина волны, используется следующая формула:
f = v / λ
Где: f — частота волны, v — скорость волны, λ — длина волны.
Пример 1:
Допустим, у нас есть волна со скоростью 320 метров в секунду и длиной волны 8 метров. Чтобы найти частоту, мы используем формулу:
f = 320 м/с / 8 м
f = 40/с
f = 40 Гц (герцы)
Итак, частота этой волны составляет 40 герц.
Пример 2:
Предположим, нам нужно найти частоту света, если известно, что его длина волны равна 3000 километров (3000 км). Скорость света в вакууме примерно равна 300 000 километров в секунду (c ≈ 300,000 км/с). Теперь используем формулу:
f ≈ 300,000 км/с / 3000 км
f ≈ 100/с
f ≈ 100 Гц (герцы)
Итак, частота света при данной длине волны составляет приблизительно 100 герц.
Приложение в реальной жизни
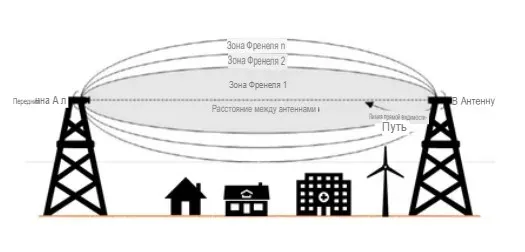
Зона Френеля — это важное понятие в области беспроводной связи, и оно имеет реальное применение в различных ситуациях. Давайте рассмотрим, как это понятие используется на практике.
Зона Френеля выглядит так:
Планирование размещения антенн: Зона Френеля помогает инженерам и проектировщикам оптимально размещать антенны в беспроводных системах связи. Путем учета длины волны и частоты сигнала они могут определить необходимый объем свободного пространства для минимизации помех в зоне Френеля.
Проектирование беспроводных сетей: В случае развертывания беспроводных сетей, таких как Wi-Fi или сотовая связь, зона Френеля используется для определения идеального местоположения и высоты антенн, чтобы обеспечить надежную связь между точками доступа и клиентскими устройствами.
Избегание помех: Зона Френеля также помогает избегать помех от преград, таких как здания, деревья или холмы. При планировании беспроводной связи необходимо учитывать, что преграды могут повлиять на объем зоны Френеля и, следовательно, на качество связи.
Развитие мобильной связи: В мобильных сетях, особенно в сотовой связи, зона Френеля учитывается при выборе местоположения базовых станций и антенн. Это помогает обеспечить хорошее покрытие и качество связи для абонентов.
Таким образом, зона Френеля — это важный элемент в планировании и оптимизации беспроводных коммуникаций, и она помогает обеспечивать стабильную и надежную связь в различных приложениях, от мобильной связи до беспроводных сетей в домах и офисах.
Как рассчитать частоту?
Для расчета частоты сигнала, вы можете использовать два различных метода, в зависимости от доступной вам информации:
Если у вас есть период волны (время, необходимое для завершения одного волнового цикла), следуйте этим шагам:
- Если период дан в других единицах времени, конвертируйте его в секунды.
- Затем разделите 1 на период в секундах.
- Результатом будет частота, измеряемая в герцах (Гц).
Например, если период волны составляет 0.02 секунды, то частота будет равна:
Частота (Гц) = 1 / 0.02 с = 50 Гц.
Если у вас есть длина волны (в метрах) и скорость волны (в метрах в секунду), используйте следующие шаги:
- Убедитесь, что длина волны и скорость волны имеют одинаковую единицу длины (например, метры).
- Разделите скорость волны на длину волны.
- Результат будет также выражен в герцах (Гц).
Например, если длина волны составляет 10 метров, а скорость волны 100 метров в секунду, то частота будет равна:
Частота (Гц) = 100 м/с / 10 м = 10 Гц.
Эти два метода позволяют вам рассчитать частоту сигнала на основе доступных данных о периоде и длине волны в соответствии с вашими потребностями.
Как мне определить длину волны по частоте?
Для определения длины волны (λ) по известной частоте (f) следуйте этим шагам:
Определите скорость волны (v). Скорость волны зависит от среды, в которой она распространяется. В вакууме скорость света приближенно равна 299,792,458 метров в секунду.
Преобразуйте частоту из герц (Гц) в обратные секунды (1/с) путем взятия обратной величины частоты:
Обратная частота (1/с) = 1 / f.
Убедитесь, что скорость волны (в метрах в секунду) и обратная частота (1/с) имеют одну и ту же единицу времени.
Разделите скорость волны на обратную частоту, чтобы определить длину волны:
Длина волны (λ) = v / (1/с).
Или, более просто:
λ = v / f.
Теперь у вас есть формула для определения длины волны по известной частоте. Например, если скорость звука в воздухе составляет приближенно 343 метра в секунду, а частота звука равна 440 Гц, то длина волны звука можно рассчитать следующим образом:
λ = 343 м/с / 440 Гц ≈ 0.7805 метра.
Таким образом, длина волны этого звука при частоте 440 Гц составляет приблизительно 0.7805 метра.
Какова связь между частотой и длиной волны?
Связь между частотой (f) и длиной волны (λ) описывается следующей формулой:
Скорость волны (v) = Частота (f) × Длина волны (λ).
Эта формула показывает, что скорость волны является произведением частоты и длины волны. Важно отметить, что скорость волны зависит от среды, в которой она распространяется. В вакууме, например, скорость света (с) составляет приближенно 299,792,458 метров в секунду.
Из этой формулы можно выразить одну из величин, если известны две другие:
Если известны скорость волны (v) и частота (f), то длину волны (λ) можно найти:
Длина волны (λ) = v / f.
Если известны скорость волны (v) и длина волны (λ), то частоту (f) можно найти:
Частота (f) = v / λ.
Если известны частота (f) и длина волны (λ), то скорость волны (v) можно найти:
Скорость волны (v) = f × λ.
Эта формула и соотношение между частотой и длиной волны очень важны в физике и инженерии и используются для анализа и описания различных типов волн, таких как световые волны, звуковые волны и другие.
В чем измеряется частота?
Частоту измеряют в Герцах (Гц). Герц — это единица измерения, которая обозначает количество циклов волны, проходящих через точку в течение одной секунды. Для удобства существуют также следующие единицы измерения частоты:
- Миллигерц (мГц) — одна тысячная (10^-3) Герца.
- Килогерц (кГц) — тысяча (10^3) Герц.
- Мегагерц (МГц) — миллион (10^6) Герц.
- Гигагерц (ГГц) — миллиард (10^9) Герц.
Название «Герц» введено в честь Генриха Рудольфа Герца, который сделал важные открытия в области электромагнитных волн и доказал их существование.
Как найти частоту волны?
Чтобы найти частоту волны, выполните следующие шаги:
Определите скорость волны: Сначала установите, с какой скоростью волна распространяется в среде. Обычно это значение известно из данных задачи или эксперимента и выражается в метрах в секунду (м/с).
Определите длину волны: Измерьте длину волны, которая представляет собой расстояние между двумя последовательными точками на волне, которые находятся в одной фазе. Длина волны также измеряется в метрах (м).
Убедитесь в единицах измерения: Убедитесь, что скорость волны и длина волны измеряются в одной и той же единице длины, например, в метрах.
Разделите скорость волны на длину волны: Выразите частоту как отношение скорости волны (V) к длине волны (λ):
Частота (f) = V / λ
Преобразуйте результат в герцы: После выполнения вычислений, убедитесь, что частота выражена в Герцах (Гц), что означает количество циклов волны в секунду. Если изначальная скорость была в метрах в секунду, а длина волны в метрах, то частота будет в Герцах.
Эти шаги помогут вам найти частоту волны на основе её скорости и длины.
Какая частота 5G?
Частота 5G варьируется в зависимости от частотного диапазона, который используется для передачи данных. 5G использует два основных частотных диапазона:
Диапазон частот 1 (Frequency Range 1 — FR1): Этот диапазон частот варьирует от 450 мегагерц (МГц) до 6 гигагерц (ГГц). В этом диапазоне находятся более низкие и средние частоты, которые используются для обеспечения покрытия в городах и на больших расстояниях. Например, частоты в диапазоне 3,5 ГГц и 2,6 ГГц являются типичными для 5G в этом диапазоне.
Диапазон частот 2 (Frequency Range 2 — FR2): Этот диапазон частот находится в диапазоне от 24,25 ГГц до 52,6 ГГц. Он также известен как миллиметровые волны (mmWave). Диапазон частот 2 используется для создания высокоскоростных и высококапацитивных сетей в плотных городских областях, но его покрытие ограничено более короткими дистанциями передачи.
Частота 5G в конкретной сети зависит от выбора частотного диапазона оператором и региональными ограничениями на использование радиочастот.
Какой цвет имеет самую высокую частоту?
Самой высокой частотой среди видимых цветов обладает фиолетовый. Его частота колеблется примерно от 670 до 750 терагерц (THz). На другом конце видимого спектра находится красный цвет, у которого частота составляет примерно от 430 до 480 терагерц (THz).
Какова связь между частотой и энергией?
Связь между частотой и энергией действительно существует и описывается формулой, которую вы упомянули:
E = h ⨉ f
Где:
- «E» — символ энергии,
- «h» — постоянная Планка, которая имеет значение около 6,626 x 10^-34 Джоулей секунду (Дж⋅с),
- «f» — частота.
Эта формула объясняет, что энергия фотона (или любой другой волны) прямо пропорциональна его частоте. То есть, чем выше частота, тем больше энергия переносится волной. Это принципиальное соотношение в физике и играет важную роль в понимании взаимосвязи между энергией и частотой электромагнитных волн.
Какая волна имеет самую высокую частоту?
Гамма-лучи представляют собой электромагнитные волны с самой высокой частотой в электромагнитном спектре, превышающей 10^19 Герц (Гц). Эти волны обладают наивысшей энергией и самыми короткими длинами волн среди всех электромагнитных волн. Их высокая энергия делает их способными отделять электроны от атомов и причинять повреждения живым клеткам. Гамма-излучение источники включают в себя такие явления, как нейтронные звезды, сверхновые взрывы, ядерные взрывы и молнии.
Как получить период из частоты?
Для того чтобы получить период из частоты, вы можете использовать следующую формулу:
T = 1 / f,
где: T — период (в секундах), f — частота (в Герцах).
Чтобы выполнить преобразование, следуйте этим шагам:
- Получите частоту в Герцах.
- Используйте формулу, разделив 1 на значение частоты.
Например, если у вас есть частота в 100 Герц, чтобы найти соответствующий период:
T = 1 / 100 = 0.01 секунда.
Таким образом, период равен 0.01 секунда при частоте 100 Герц.
Истории развития частоты
История развития понимания и использования частоты богата научными открытиями и технологическими прорывами. Вот несколько ключевых моментов и интересных фактов из истории развития частоты:
Открытие Герцем (1887 год):
- Ключевой момент: Нильс Герц, немецкий физик, провел эксперименты, доказавшие существование электромагнитных волн. Его исследования позволили измерять и оценивать частоту этих волн. Единица измерения «герц» была названа в его честь.
- Интересный факт: Эксперименты Герца стали основой для развития радиосвязи и беспроводной передачи данных.
Развитие радиосвязи (20 век):
- Ключевой момент: В 20 веке радио стало широко распространенным средством связи. Разработка радиоаппаратуры и трансмиссии сигналов на разных частотах сделала радиовещание и радиосвязь доступными для массового использования.
- Интересный факт: В 1901 году Гуглиельмо Маркони осуществил первую беспроводную передачу сообщения через Атлантику, используя радиоволны.
Развитие электроники и полупроводников (вторая половина 20 века):
- Ключевой момент: Развитие электронных компонентов и полупроводников позволило создавать частотные генераторы и усилители, способные работать на очень высоких и низких частотах. Это привело к развитию современной радиоэлектроники.
- Интересный факт: Развитие микроэлектроники привело к созданию современных микропроцессоров, которые работают на очень высоких частотах и играют важную роль в современной технике.
Развитие современных сетей связи (конец 20 века — начало 21 века):
- Ключевой момент: Внедрение оптоволоконных кабелей и цифровых технологий в сети связи позволило передавать информацию на высоких частотах с большой пропускной способностью. Это стало основой для интернета, цифрового телевидения и мобильной связи.
- Интересный факт: С появлением сетей 5G возможна передача данных на еще более высоких частотах, что обеспечивает более высокую скорость и надежность связи.
Применение в научных исследованиях (все века)
Частота играет важную роль в научных исследованиях в различных областях, включая астрономию, физику, медицину и многие другие. Измерение и анализ частоты позволяют ученым изучать природные явления и разрабатывать новые методы диагностики и лечения.
История частоты отражает постоянное развитие технологий и научных знаний. Открытия и применения в этой области оказали значительное воздействие на современный мир и продолжают влиять на развитие новых технологий и научных открытий.
 SAS инструменты Сайт с 1000 ми полезных инструментов и калькуляторов SAS
SAS инструменты Сайт с 1000 ми полезных инструментов и калькуляторов SAS